Решение. 1. Геометрические характеристики швеллера относительно его собственных центральных осей (рис
1. Геометрические характеристики швеллера относительно его собственных центральных осей (рис. б) согласно ГОСТ 8240-72 следующие:
площадь A1 = 23,4 см2,
высота сечения h1 = 20 см,
моменты инерции 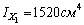 ,
, 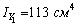 ,
,
абсцисса центра тяжести швеллера  .
.
(ГОСТ прокатных профилей есть в приложениях всех литературных источников, приведённых в списке литературы).
Здесь и далее индекс в нижнем правом углу означает номер простой составляющей сечения. Например, швеллер, согласно принятой в задаче нумерации, имеет номер 1.
Геометрические характеристики прямоугольника относительно его собственных центральных осей (рис. в) следующие:
- площадь  ,
,
- моменты инерции относительно собственных центральных осей
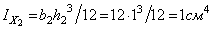 ,
, 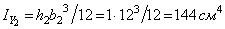 .
.
2. Построение сечения в масштабе (см. рисунок 1, а).
3. Определение координаты центра тяжести сечения.
- Строим вспомогательную систему координат. В качестве вспомогательной системы координат выбираем центральные оси швеллера 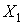 и
и  .
.
- Определяем координаты центра тяжести сечения относительно вспомогательной системы координат. Для рассматриваемого сечения необходимо вычислить только одну координату 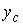 , так как другая координата
, так как другая координата 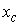 известна. Поскольку центр тяжести всего сечения должен лежать на прямой, соединяющей центры тяжести простых составляющих (это правило действительно для сечений, состоящих их двух частей), то в нашем случае центр тяжести лежит на оси
известна. Поскольку центр тяжести всего сечения должен лежать на прямой, соединяющей центры тяжести простых составляющих (это правило действительно для сечений, состоящих их двух частей), то в нашем случае центр тяжести лежит на оси 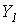 (см. рисунок 1, а), а значит координата
(см. рисунок 1, а), а значит координата 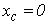 .
.
Координата центра тяжести (к. ц. т.) сечения 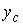 определяется по формуле:
определяется по формуле:
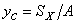 ,
,
где А – площадь всего сечения;  - статический момент всего сечения относительно оси
- статический момент всего сечения относительно оси 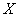 . Для рассматриваемого примера статический момент сечения следует обозначить, как
. Для рассматриваемого примера статический момент сечения следует обозначить, как  , так как
, так как 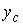 определяется относительно оси
определяется относительно оси  .
.
Рассматриваемое сечение сложное. Для определения статического момента сложного сечения существует формула:
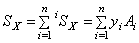 ,
,
где n – число простых составляющих сложного сечения; 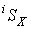 - статический момент i –й составляющей сложного сечения;
- статический момент i –й составляющей сложного сечения; 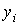 ,
, 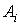 - координата центра тяжести и площадь i –й составляющей сложного сечения. Применительно к нашей задаче формула примет следующий вид:
- координата центра тяжести и площадь i –й составляющей сложного сечения. Применительно к нашей задаче формула примет следующий вид:
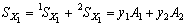 .
.
Так как координата y в прямоугольной системе координат представляет собой кратчайшее расстояние (перпендикуляр) от центра тяжести соответствующей фигуры до оси X, то:
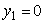 ,
, 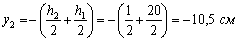 ;
;
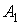 и
и  определены в пункте I. Подставим в формулу полученные значения:
определены в пункте I. Подставим в формулу полученные значения:
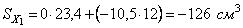 .
.
Площадь сложного сечения 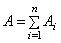 . Тогда для рассматриваемого случая:
. Тогда для рассматриваемого случая:
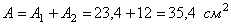 .
.
Следовательно, 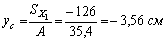 .
.
Для случая, когда неизвестной является координата 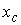 , задача решается аналогично с учётом соответствующих изменений.
, задача решается аналогично с учётом соответствующих изменений.
- Показываем на чертеже центральные оси всего сечения XC и YC. Причём эти оси строим параллельно вспомогательным осям, как показано на рис. а.
4. Проводим проверку правильности определения центра тяжести сечения.
В основе проверки лежит положение о том, что статические моменты сечения относительно центральных осей равны нулю. Значит, в нашем случае следует вычислить статические моменты сечения относительно полученных центральных осей XC и YC, при этом координаты ц. т. простых составляющих относительно этих осей:
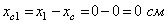 ,
, 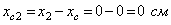 ;
;
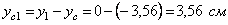 ,
,
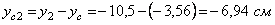 .
.
Статические моменты сечения относительно осей XC и YC:

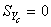 .
.
Иными словами, координаты ц. т. всего сечения вычислены правильно.
5. Определяем главные центральные моменты инерции сечения.
- Вычисляем центробежный момент инерции всего сечения.
Ось  - центральная ось всего сечения и
- центральная ось всего сечения и 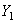 ,
, 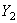 - центральные оси простых составляющих – совпадают. Оси
- центральные оси простых составляющих – совпадают. Оси  и
и 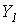 - главные оси швеллера, значит центробежный момент инерции швеллера относительно них
- главные оси швеллера, значит центробежный момент инерции швеллера относительно них 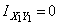 . Оси
. Оси 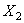 и
и 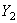 - главные оси прямоугольника (так как оси
- главные оси прямоугольника (так как оси 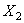 и
и 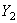 - оси симметрии прямоугольника), то есть
- оси симметрии прямоугольника), то есть 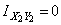 . В этом случае центробежный момент инерции всего сечения в соответствии с формулой изменения центробежных моментов инерции при параллельном переносе осей (см. теорию):
. В этом случае центробежный момент инерции всего сечения в соответствии с формулой изменения центробежных моментов инерции при параллельном переносе осей (см. теорию):
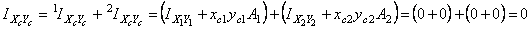 .
.
- Находим главные оси всего сечения.
Так как центробежный момент инерции сечения относительно главных осей равен нулю, то в нашем случае оси XC и YC - главные оси инерции всего сечения.
- Вычисляем главные центральные моменты инерции всего сечения.
Поскольку главными центральными моментами инерции являются моменты инерции относительно главных центральных осей, то вычисления моментов инерции будем производить относительно осей XC и YC.
Воспользовавшись формулой определения осевых моментов инерции сложного сечения и формулой перехода между параллельными осями для осевых моментов инерции (см. теорию), получим
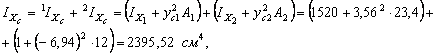
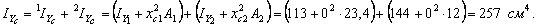
6. Определяем значения осевых моментов сопротивления.
Осевые моменты сопротивления в нашем случае вычисляются по формулам
 ;
; 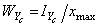 ,
,
где xmax и ymax - расстояния от соответствующих осей до наиболее удалённых точек сечения (см. рис. а).
Здесь: 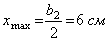 ;
;
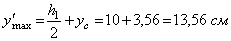 ;
;
 .
.
Тогда: 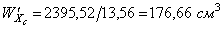 ;
;
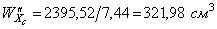 ;
;
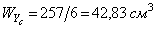 .
.
Дата добавления: 2015-08-08; просмотров: 2102;
