Решение. Вычерчиваем сечение в масштабе на листе чертежной или миллиметровой бумаги
Вычерчиваем сечение в масштабе на листе чертежной или миллиметровой бумаги. Обозначим отдельные элементы: I - двутавр; II – пластина; III – неравнобокий уголок (рис. 2). Затем проводим центральные оси каждого сечения X1, Y1; X2, Y2 и X3, Y3.
Из сортамента выписываем все необходимые для расчета данные:
1. Двутавр №20 (ГОСТ 8239 – 89).
Как видим из чертежа (рис.2), двутавр расположен горизонтально, а в сортаменте – вертикально. По этой причине принимаем осевые моменты инерции 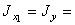 115 см4,
115 см4, 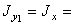 1840 м4,
1840 м4,
b1 = h = 20 см, h1 = b = 10 см, где Jx, Jy, h и b – числовые данные из сортамента. Площадь поперечного сечения А1 = 26,8 см2.
2. Пластина (прямоугольник): b2 = 16 см; h2 = 2 см.
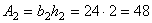 см2.
см2.
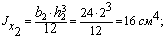
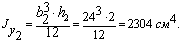
3. Уголок неравнобокий 100х63х6 мм (ГОСТ – 8510 – 86):
А3 = 9,58 см3; 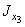 = 98,3 см4;
= 98,3 см4; 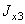 = 30,6 см4;
= 30,6 см4; 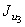 = 18,2 см4;
= 18,2 см4;
х0 = 1,42 см; у0 = 3,23 см; 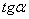 = 0,393; b3 = 0,3 см; h3 = 10 см.
= 0,393; b3 = 0,3 см; h3 = 10 см.
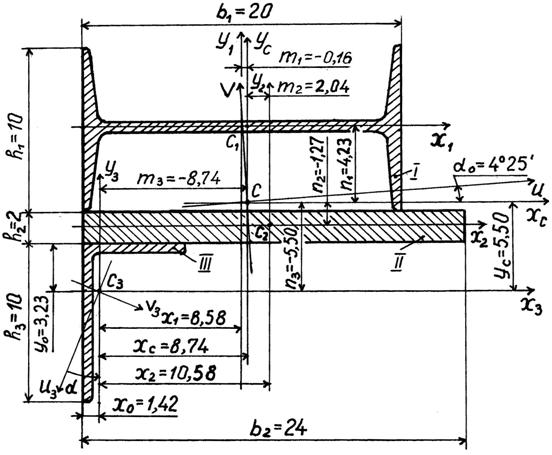
Рис.2
1. Определение центра тяжести сечения. Выбираем в качестве вспомогательных осей – оси уголка х3, у3. Определяем относительно этих осей координаты центров тяжести сечений:
- для двутавра: х1 = b1/2 – х0 = 20/2 – 1,42 = 8,58 см;
у1 = у0 + h2/2+h1/2 = 3,23 + 2/2+11/2 = 9,73 см;
- для пластины: х2 = b2/2 – х0 = 24/2– 1,42 = 10,58 см;
у2 = у0 + h2/2 = 3,23 +2/2 = 4,23 см;
- для уголка: х3 = 0; у3 = 0.
Вычисляем координаты центра тяжести составного сечения по формулам:
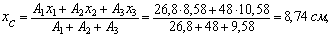

Откладываем от вспомогательных осей х3, у3 координаты центра тяжести хС, уС и через полученную точку С проводим центральные оси ХС и YС параллельно вспомогательным осям.
2. Вычисление осевых ( 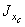 ,
, 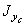 ) и центробежного (
) и центробежного ( 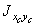 ) моментов инерции сечения относительно центральных осей (XС , YС). Применим формулы для вычисления моментов инерции составного сечения при параллельном переносе осей:
) моментов инерции сечения относительно центральных осей (XС , YС). Применим формулы для вычисления моментов инерции составного сечения при параллельном переносе осей:
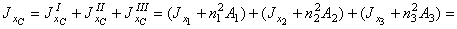
= (115 + 4,232×26,8) + (16 + (-1,27)2×48) + (98,3 + (-5,50)2×9,58) =594 + 93,4 + 388 = 1075 см2,
где n1, n2 и n3 – расстояния от центральной оси ХС до осей х1, х2 и х3, соответственно. Т.е. имеем:
n1 = у1 – уС = 9,73 – 5,50 = 4,23 см;
n2 = -(уС – у2) = -(5,50 – 4,23) = -1,27 см;
n3 = - уС = -5,50 см.
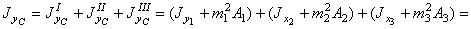
= (1840 + (-0,16)2×26,8) + (2304 + 2,042×48) + (30,6 + (-8,74)2×9,58) = 1841 + 2504 + 762 = 5107 см4,
где m1, m2 и m3 – расстояние от центральной оси YС до осей у1, у2 и у3, соответственно. Т.е. имеем:
m1 = -(хС – х1) = -(8,74 – 8,58) = -0,16 см;
m2 = х2 – хС = 10,58 – 8,74 = 2,04 см;
m3 = -хС = -8,74 см.
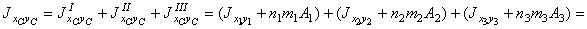
=(0 + 4,23×(-0,16)×26,8) + (0 + (-1,27)×2,04×48) + (31,5 + (-5,50)×(-8,74)×9,58) = -18,1 – 124,3 + 400 = 318 см4.
При вычислении центробежного момента инерции 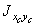 следует учесть, что для симметричных сечений (двутавр, швеллер, пластина) центробежные моменты инерции относительно их собственных центральных осей равны нулю, т.к. оси симметрии являются главными осями. Тогда
следует учесть, что для симметричных сечений (двутавр, швеллер, пластина) центробежные моменты инерции относительно их собственных центральных осей равны нулю, т.к. оси симметрии являются главными осями. Тогда 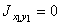 ,
, 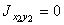 .
.
Для неравнобокого уголка ось U3 и ось V3, проведенная нами через центр тяжести О3 перпендикулярно первой оси, являются главными центральными осями уголка (см. рис.2). Следовательно, центробежный момент инерции уголка относительно этих осей равен нулю.
Оси х3, у3 не являются главными центральными осями. Поэтому 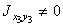 . Для его вычисления воспользуемся известной формулой:
. Для его вычисления воспользуемся известной формулой:
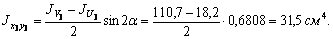
При этом для вычисления неизвестного главного момента инерции 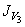 воспользуемся зависимостью:
воспользуемся зависимостью:
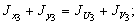
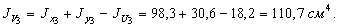
Для определения угла a из сортамента имеем 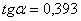 . Тогда
. Тогда 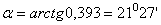 .
.
Угол  в данном случае положителен, т.к. поворот главных центральных осей V3, U3 до совмещения их с осями х3, у3 выполнен против часовой стрелки (см. рис.2).
в данном случае положителен, т.к. поворот главных центральных осей V3, U3 до совмещения их с осями х3, у3 выполнен против часовой стрелки (см. рис.2).
Для определения знака центробежного момента инерции для равнобоких и неравнобоких уголков в зависимости от их положения удобно пользоваться также данными рис.3.
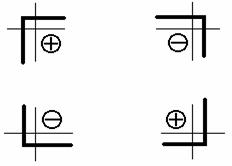
Рис.3
|
3. Определение положения главных центральных осей инерции.
Определяем угол 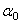 по формуле:
по формуле:
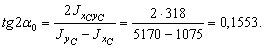
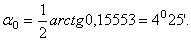
|
Откладываем от оси XС угол 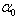 против часовой стрелки и проводим взаимно перпендикулярно главные оси для составного сечения U и V, соответственно.
против часовой стрелки и проводим взаимно перпендикулярно главные оси для составного сечения U и V, соответственно.
4. Вычисление главных центральных моментов инерции. Для их вычисления используем формулу:
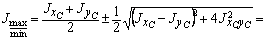
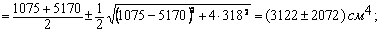
Jmax = 5104 см4; Jmin = 1050 см4.
Т.к. 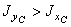 , то
, то 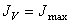 , а
, а 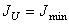 .
.
Для проверки правильности расчетов воспользуемся формулой для вычисления центробежного момента инерции. Вычислим его относительно главных центральных осей U и V (JUV = 0):
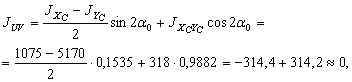
где 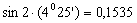 ;
; 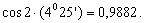
Ошибка в инженерных расчетах не должна превышать 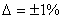 . Проверяем расчеты по формуле:
. Проверяем расчеты по формуле:
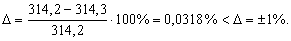
Дата добавления: 2015-08-08; просмотров: 2222;
