Пример 6.
Для сложных составных поперечных сечений, не содержащих осей симметрии, предлагается следующий порядок расчета.
1) Сначала вычерчивается поперечное сечение. Случайные оси х, у ставим так, чтобы все точки поперечного сечения находились в 1-м квадранте (рис.1). Каждому прокатному профилю присваивается порядковый номер. Наносим местные оси координат хi, уi, проходящие через известные центры тяжести i–го профиля. Оси хi, уiпараллельны случайным осям х, у соответственно.
2) Наносим на рисунок известные размеры сечения, взятые из задания или из соответствующих таблиц сортамента прокатной стали.
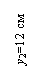
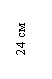
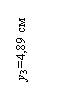
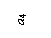
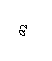
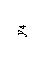
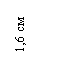
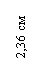
3) Вводим обозначения: хi, уi – абсцисса и ордината центра тяжести соответственно i–го профиля относительно случайных осей х, у; Аi – площадь сечения i–го профиля,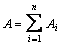 
– площадь поперечного сечения всего составного сечения;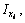 
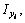
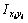– осевые и центробежные моменты инерции i–го профиля относительно местных осей хi, уi.
4) Следуя предложенной методике, выпишем геометрические характеристики для поперечного сечения, изображенного на рис. 1:
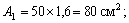
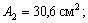
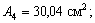
х1 = 25 см; х2 = 43,42 см; х3 = 36,11 см; х4 = 5,32 см;
у1 = 24,8 см; у2 = 12 см; у3 = 4,89 см; у4 = 21,64 см;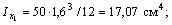 
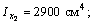
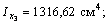
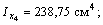
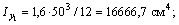
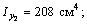
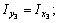
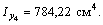
5) С помощью формул
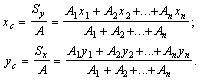
находим координаты центра тяжести всего поперечного сечения:
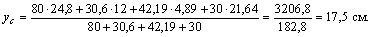
6) Наносим оси хс, ус, которые проходят через центр тяжести С всего составного поперечного сечения и определяем расстояния между осями хс и хi, а также между осями ус и уi:
а1 = у1 – ус = 24,8 – 17,5 = 7,3 см; b1 = х1 – хс = 25 – 27,4 = –2,4 см;
а2 = у2 – ус = 12 – 17,5 = –5,5 см; b2 = х2 – хс = 43,42 – 27,4 = 16,02 см;
а3 = у3 – ус = 4,89 – 17,5 = –12,61 см; b3 = х3 – хс = 36,11 – 27,4 = 8,71 см;
а4 = у4 – ус = 21,64 – 17,5 = 4,14 см; b4 = х4 – хс = 5,32 – 27,4 = –22,08 см.
7) Используя формулы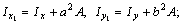 
получаем выражения для вычисления осевых моментов инерции относительно центральных осей хс и ус всего поперечного сечения:
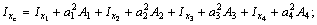
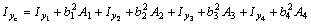
или окончательно:
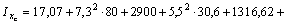
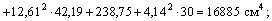
По формуле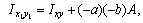 
находим значение центробежного момента инерции относительно осей хс, ус:
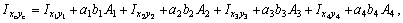
где, согласно рис. 1, имеем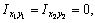 
так как швеллер и полоса имеют оси симметрии х2 и х1, у1 соответственно.
Для вычисления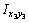 
для равнополочного уголка предварительно выпишем из таблицы сортамента «Уголки стальные горячекатаные равнополочные» 
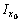= 2093 см4, 
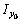= 540 см4, 
, 
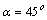(рис. 2, а).
Тогда формула 
принимает вид:
Для вычисления 
для неравнополочного уголка (рис. 2, б) предварительно выпишем из таблицы сортамента
= 238,75 см4,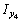 
= 784,22 см4, Iuv = 0, Iu = 142 см4, 
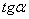= 0,388
и затем, согласно формуле 
получаем:
Таким образом, формула для рассматриваемого случая принимает вид:
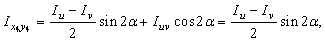
где 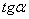= 0,388; 
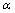= –21о12/ (рис.2, б), тогда
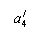
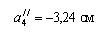
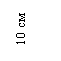
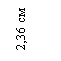
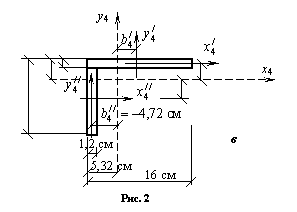
Значение центробежного момента можно вычислить, используя формулу 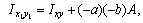. Для этого рассмотрим рис. 2, в. Разобьем уголок на два прямоугольника с
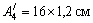и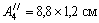 
.
В этом случае по формуле 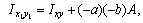получаем
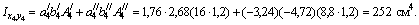
Как видно, результаты очень близки по значениям.
Теперь можно приступить к определению центробежного момента всего составного сечения относительно осей хс, ус:
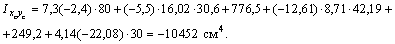
8) Главные оси инерции можно построить, повернув центральные оси хс, ус на угол 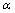(рис. 1):
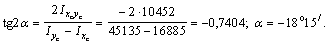
9) Величины главных моментов инерции определяем по формуле
Окончательно получаем, что Imax = 48582 см4, Imin = 13438 см4.
Полученные значения удовлетворяют условию :
Таким образом, определены все геометрические характеристики сложного составного поперечного сечения, показанного на рис.1.
Дата добавления: 2015-08-08; просмотров: 766;