Решение. 1. Определение моментов инерции относительно центральных осей хСy.
1. Определение моментов инерции относительно центральных осей хСy.
По таблице сортамента имеем:
швеллер № 22: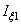 
= 2330 cм4, 
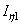= 187 cм4, А1 = 28,8 см2;
уголок 100х100х10: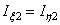 
= 179 cм4, А2 = 19,2 см2;
центробежный момент инерции уголка относительно 
= 105 cм4.
Учитывая, что центральные оси xy проведены параллельно собственным осям элементов фигуры, для вычисления осевых и центробежного моментов инерции всего сечения воспользуемся формулами, представляя все необходимые вычисления в табличной форме:
| Номер элемента | Координаты центра тяжести, см | Площадь Аi, см4 | Моменты инерции площадей, см4 | |||||||||
| 
| 
| ||||||||||
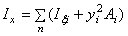
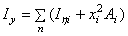
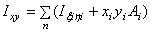
| xi | yi |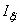 
| 
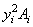
| Ixi | 
| 
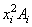
| Iyi |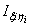 
| xiyiAi | Ixiyi | ||
| -2, | -3, | 28,8 | ||||||||||
| 3, | 4, | 19,2 | ||||||||||
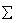
| 3278 | 688 | 603 |
2. Определение главных центральных моментов инерции сечения. По формуле имеем
,
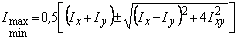Отсюда Imax = I1 = 3412 см4, Imin = I2 = 555 см4.
Ориентация максимальной главной оси определяется по формуле
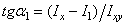= (3278-3412)/603 = -0,222,
откуда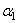 
= -12°30'.
3. Построение эллипса инерции. Главные радиусы инерции равны
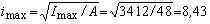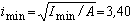см;
см.
Отложив радиусы инерции перпендикулярно к соответствующим осям в том же масштабе, в каком вычерчена фигура, строим на них, как на полуосях, эллипс инерции.
Дата добавления: 2015-08-08; просмотров: 666;