Решение. Разбиваем фигуру на части, геометрические характеристики которых можно взять из таблиц сортамента, на швеллер и уголок; через их центр тяжести c1 и c2
Разбиваем фигуру на части, геометрические характеристики которых можно взять из таблиц сортамента, на швеллер и уголок; через их центр тяжести c1 и c2 проводим центральные оси z1, y1 и z2, y2, параллельные их сторонам. Поскольку z1 - ось симметрии швеллера, то она и ось y1 являются его главными центральными осями. Главная центральная ось уголка v-v образует с его центральной осью z2 угол 
.
Из таблиц сортамента имеем:
Для швеллера №24 F1=30,6 см2
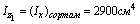
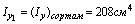
координаты центра тяжести
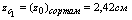
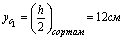
h=24 см b=9 см
Для уголка №14/9 F2=22,2 см2
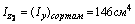
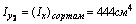
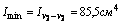
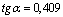
координаты центра тяжести
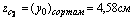
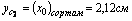
1) Определим координаты центра тяжести всего сечения, для этого принимаем за исходные оси главные центральные оси швеллера z1 и y1 и согласно (4.4) получаем:
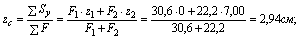
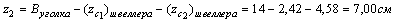
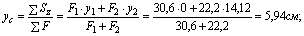
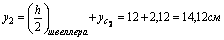
Через центр тяжести C проводим центральные оси zc и yc, параллельные проведенным ранее центральным осям швеллера и уголка.
Для проверки правильности определения координат центра тяжести, вычислим статические моменты относительно центральных осей zc и yc, которые должны быть равны нулю.
Получаем:
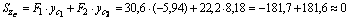
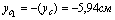
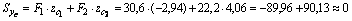
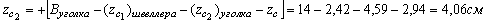
2) Вычислим осевые и центробежный моменты инерции всего сечения в системе центральных осей zc, yc по формулам:
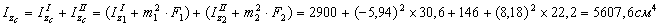
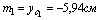
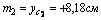
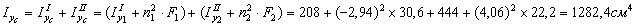
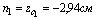
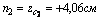
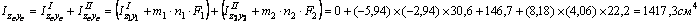
для швеллера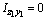 
, т.к. оси z1 и y2 являются для швеллера главными центральными; для уголка 
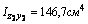согласно сортамента.
3) Определяем угол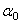 
наклона главных центральных осей u и v относительно центральных осей zc, yc:
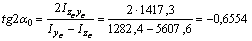
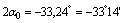
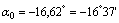
Поскольку угол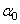 
отрицательный, он откладывается по ходу часовой стрелки, а т.к. 
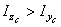, то поворотом оси z на угол, меньший 45°, мы получим направление главной центральной оси u, относительно которой главный момент инерции максимален Iu=Imax.
4) Главные моменты инерции определяем по формулам
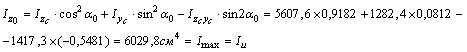
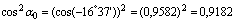
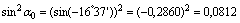
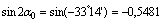
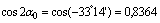
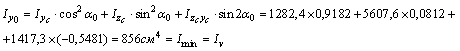
Проверки: а) Определяем центробежный момент инерции относительно главных центральных осей 
, который должен быть равен нулю:
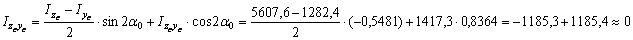
б) Определим главные центральные моменты инерции Iu и Iv по формулам:
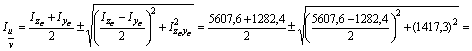
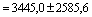
Iu=Imax=3445,0 + 2585,6 = 6030,6 см4
Iv=Imin=3445,0 - 2585,6 = 859,4 см4
Максимальное расхождение составляет:
.
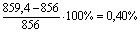в) Должно удовлетворяться условие:
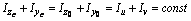
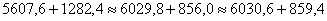
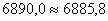
Расхождение составляет:
.
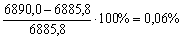5. Определение моментов сопротивления сечения.
Наиболее удаленными точками от осей u и v являются точки A и B:
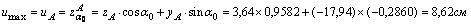
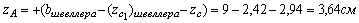
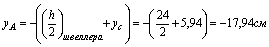
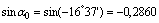
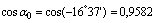
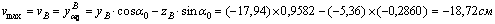
yB = yA = -17,94 см
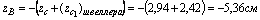
По формулам получаем:
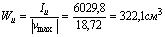
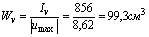
6. Радиусы инерции вычисляются по формулам (4.35), (4.36):
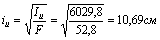
F = F1 + F2 = 30,6 +22,2 = 52,8 см2
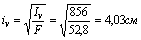
Откладывая отрезки iu=10,69см и iv=4,03см перпендикулярно соответствующим осям, строим на них, как на полуосях, эллипс инерции (см. рис.).
Дата добавления: 2015-08-08; просмотров: 1066;