Диф. ур-я первого порядка. Общее и частное решение. Теорема существования и единственности решения

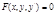
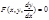
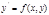- ур-е относительно одной производной

Теорема существования единственности решения: если в ур-и 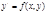ф-я f(x,y) и её частная производная по y 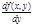непрерывны в некот. области d, содержащей точку M₀(x₀,y₀) принадлеж. D, то существует единственное решение этого ур-я 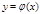, кот. удовлетворяет условию: при x=x₀ y=y₀.

График решения ур-я наз.интегральной кривой.

Условие y 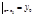– начальное условие.

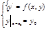образует задачу Коши

Общим решениемдиф.ур-я 1 порядка наз. всякая функция вида 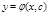, зависящая от 1 произвольной постоянной С и удовлетворяющая условиям:

а) эта ф-я удовлетворяет условию при любых значениях const C;

б) каково бы ни было нач. условие y 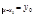, можно найти такое значение const С=С₀, что ф-я 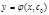будет удовлетворять нач. условию.

Частным решением диф.ур-я наз. любая ф-я 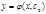, кот. получается из общего решения, если вместо произвольной константы подставить конкретное значение.

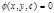- общее решение

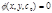- частное решение

Пример 1.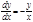

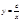- общее решение

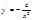
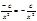
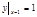
с=1.

Решить диф.ур-е значит найти его общее решение, если не задано нач. условие; если задано условие – найти частное решение, кот.удовлетв.нач.условию.