Сравнения. Арифметические приложения теории сравнений. Теорема о длине периода десятичной дроби
Целые числа a и b называются сравнимыми по модулю m, если разность a-b делится на m. Это соотношение записывается так: a≡≡b(mod m).
Например: 17≡2 (mod 5), -7≡25 (mod 8).
Теорема: число a сравнимо с b по модулю m, тогда и только тогда, когда a и b имеют одинаковые остатки при делении на m.
Целые числа a и b называются сравнимымипо модулю m, если остатки от деления этих чисел на m равны.
Из определений сравнимости следует, что число сравнимо по модулю со своим остатком при делении на модуль.
Сравнимые по данному модулю числа имеют с ним один и тот же НОД. Обратное утверждение неверно.
Все целые числа сравнимы между собой по модулю 1.
Свойства сравнений:
1.Отношение сравнения есть отношение эквивалентности на множестве целых чисел Z:
- отношение сравнения рефлексивно: a≡a(mod m);
- отношение сравнения симметрично: если a≡b(mod m), то b≡a(mod m);
- отношение сравнения транзитивно: если a≡b(mod m) и b≡c(mod m), то a≡c(mod m)
2.Если a≡b(mod m) и c≡d(mod m), то справедливо сравнение a±c=b±d(mod m)
3.Если a≡b(mod m) и k – произвольное целое число, то ka≡kb(mod m)
4.Если ka≡kb(mod m) и (k,m)=1, то a≡b(mod m)
5.Если a≡b(mod m) и k – произвольное натуральное число, то ka≡kb(mod k m)
6.Если ka≡kb(mod k m) и k – произвольное натуральное число, то a≡b(mod m)
7.Если a≡b(mod m) и c≡d(mod m), то справедливо сравнение ac≡bd(mod m)
8.Если a≡b(mod m), то при любом целом n≥0 an≡bn(mod m)
9.Если a≡b(mod m) и f(x)=c0+c1x+K+cnxn – произвольный многочлен с целыми коэффициентами, то f(a)≡f(b)(mod m)
10.Если a≡b(mod m1), a≡b(mod m2),…, a≡b(mod mn), то a≡b(mod m), где m=[m1, m2, K, mn]
11. В сравнении можно отбрасывать или добавлять слагаемые, делящиеся на модуль
Полные системы вычетов, их виды и св-ва. ПСВm-система чисел, взятых по одному из каждого класса вычетов по mod m. Полных систем вычетов сущ.бесконечно много.
Пусть m=4 ПСВm: {0,1,2,3}-полная система наименьших неотрицательных вычетов (ПСННВm)
{4,5,6,7}-остатки 
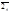={2+4t} t=-2
{-4, 1, -2, 23}
Образуем систему по сл. принципу: в каждом классе выберем число, у кот. абсолютная величина явл.неизвестной.
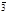= {-1,37,..}
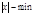
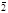={+-2} 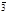={3+4t} t=0 (m0-3) t=1 (m0-1)
{0,1,2(или -2),-1}-полная система абсолютно наименьших вычетов (ПСАНВm).
Свойства ПСВm:
1)любая система из m целых чисел {a1,a2,..,am}попарно не сравнимых между собой по mod m явл. полной системой вычетов по этому модулю.
2)если {r1,r2,..,rm} (1) – какая-нибудь ПСВm, число а взаимно просто с модулем (a,m)=1, ab-любое целое, тогда система чисел {ar1+b,ar2+b,..,arm+b}(2) тоже образует ПСВm.
Приведённые системы вычетов и их св-ва.
Св-во: если a и b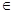 
r по mod m, a 
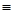b (mod m) , НОД (a,m)=(b,m)
a=mt1+r=>по св-ву НОД (a,m)=(m,r)
b=mt2+r=>по св-ву НОД (b,m)=(m,r)
ð (a,m)=(b,m)
Класс вычетов по mod m наз. взаимно простым с модулем, если все числа из этого класса взаимно просты с модулем.
ПрСВm-система чисел, взятых по одному из каждого класса вычетов взаимно простого с m.
Очевидно, что число чисел в ПрСВ по mod m = значению функций Эйлера φ(m)
ПрСВ4. φ(4)=φ(22)=2*(2-1)=2
ПрСВ4={0,1,2,3} ПрСВ4={1,3}, т.к. 0 и 2 не взаимно просты с 4.
Свойства ПрСВm:
-любые φ(m) попарно не сравнимы между собой и взаимно простые с m чисел составляют ПрСВm.
-если r1, r2,…,rφ(m) -какая-нибудь ПрСВm и число (a,m)=1, то система чисел ar1, ar2,…,arφ(m) -тоже ПрСВm.
Пример: φ(10)=4, а=7 (7,10)=1. Каков остаток от деления числа 710=q+r
74=49*49=(50-1)2=2500-100+1=2401
2401=10*240+1
7φ(10)≡1(mod 10)
74=72*72=9*9≡81≡1(mod 10)
Функция Эйлера и ей свойства, формулы для вычисления.Функция Эйлера φ(n)- число натуральных чисел, не превосходящих n и взаимно простых с n.
.
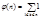Пример: 1) 1,2,3,4,5 числа <5 и взаимно простые с ним φ(5)=4
2) φ(10)=4- кол-во чисел <10 и взаимно простых с 10.
Если p-простое, то φ(p)=p-1, φ(101)=100
p-простое, α≥1,φ(pα):
1) подсчитаем число натуральных чисел ≤p2 и делящихся на p. Если a/р, то а=p*t. p,2p,3p,..
max pt*pt≤pα, t-число таких чисел, t≤pα/p, t=pα-1.
2)α(pα)=pα*pα-1
Α(p)=p-1, p – простое, φ(pα)=pα-1(p-1)
Можно доказать, что если a и p-числа взаимно простые, то φ(a,b)=φ(a)*φ(b). Т.к.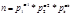 
, то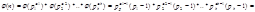 
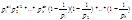
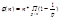
Пример: 1) φ(10)=10(1-1/2)(1-1/5)=4
2) φ(100)=100(1-1/2)(1-1/5)=100*1/4*4/5=40
Дата добавления: 2015-07-30; просмотров: 3409;