Методика изучения геометрических преобразований

Цель изучения: осознание учащимися понятия геометрического преобразования, типов и примеров геометрических преобразований, способов их осуществления и идеи их применения в геометрии и для решения задач.

Изучения геометрических преобразований:

1)Подготовительный этап – рассмотрение примеров фигур, обладающих свойством быть полученной одна из другой с помощью данного преобразования.

2)построение плоских фигур.

3)решение задач на узнавание.

4)выявление свойств преобразования, их доказательство.

5)решение задач на усвоение понятия данного преобразования и его свойств.

6)примеры применения данного преобразования к решению задач и доказательству теорем.

7)выявление действий по применению теории к решению задач, их последовательности и ситуаций применения.

8)обобщение выявленных действий в виде приёма к решению задач на плоскости.

9)применение полученного приёма к решению задач на плоскости.

10)примеры геометрических преобразований пространства и фигур в пространстве.

11)примеры применения полученного приема к решению задач в пространстве.

12)обобщение ситуаций применения метода геометрических преобразований к решению задач.

Геометрическое преобразование: каждой точке некоторого (линии, поверхности, пространства) ставится в соответствие другая точка того же многообразия.

Движение - геометрическое преобразование, сохраняющее расстояния между точками.

Подобие геометрическое преобразование, при котором расстояния между точками изменяются в одно и то же число раз.

Свойства движений

Композиция движений – движение

Преобразование, обратное движению, – движение

Три точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения

Пусть движение переводит три точки A, B, C, лежащие на одной прямой, в точки А`, B` и C`, для определенности положим, что точка B лежит между точками A и C. Тогда выполняются равенства

А`B`=АВ, B`C`=ВС, А`C`=АС, АС=АВ+ВС

Отсюда А`C`= А`B`+ B`C`. Это означает, что точка B` лежит между точками А` и C`.

При движении прямые переходят в прямые. При движении полупрямые переходят в полупрямые. При движении отрезки переходят в отрезки.

Свойства преобразования подобия:

-Три точки, лежащие на прямой, при преобразовании подобия переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.

-При преобразовании подобия прямые переходят в прямые

-При преобразовании подобия полупрямые переходят в полупрямые

-При преобразовании подобия отрезки переходят в отрезки

-При движении и преобразовании подобия сохраняются углы между полупрямыми

Поворотом фигуры F вокруг центра O на данный угол 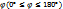в данном направлении называется такое ее преобразование, при котором каждой точке X фигуры F сопоставляется точка X` так, что  XOX`= φ и луч OX` откладывается от луча OX в заданном направлении. Точка O называется центром поворота, а угол φ – углом поворота

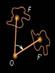
Поворот является движением.

Преобразование фигуры F, при котором произвольная ее точка M (x; y) переходит в точку М`(х+а; у+b), где a и b – одни и те же для всех точек (x; y), наз. параллельным переносом. Параллельный перенос сохраняет расстояние, а значит является движением.

Любое движение в пространстве может быть получено с помощью не более чем трех осевых симметрий. Поворот может быть представлен в виде двух симметрий.

Классификация движений:

Любое движение в пространстве можно получить, выполняя последовательно

-либо поворот вокруг прямой и перенос вдоль этой прямой (винтовой поворот),

-либо поворот вокруг прямой и отражение в плоскости (зеркальный поворот),

-либо отражение в плоскости и перенос вдоль этой плоскости (скользящее отражение)

Поворот вокруг оси. Порядок оси – число поворотов вокруг оси, которыми фигура самосовмещается. Если фигура самосовмещается в результате последовательно выполненных поворотов вокруг прямой а и затем отражения в плоскости, перпендикулярной прямой а, то а – ось зеркальной симметрии Октаэдр.

Две фигуры называются равными, если они движением переводятся одна в другую.

Треугольники подобны, если соответственные углы равны, а сходственные стороны пропорциональны или они переводятся друг в друга преобразованием подобия

Признак подобия треугольников по двум углам. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Признак подобия треугольников по двум сторонам и углу между ними.Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, и углы, образованные этими сторонами, равны, то треугольники подобны.

Признак подобия треугольников по трем сторонам.Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

34. Начала систематического курса стереометрии

Методика изучения аксиом стереометрии

Построение системы аксиом стереометрии происходит по двум направлениям: 1) переформулирование аксиом планиметрии для пространства; 2) добавление новых «специфических» аксиом стереометрии.

Первое из них осуществляется через принятие аксиомы: «В каждой плоскости пространства справедливы (выполнимы) все аксиомы планиметрии». Второе состоит в формулировании нескольких аксиом принадлежности для пространства.

Свойства плоскости в пространстве выражают аксиомы:

С1.Какова бы не была плоскость, существуют точки, принадлежащие и не принадлежащие этой плоскости.

С2.Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

С3.Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.