Теоремы Эйлера и Ферма и их применение

Теорема Эйлера. Для любого целого + числа а (a,m)=1 выполняется сравнение .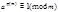

Док-во т. Эйлера: рассмотрим ПрСВm 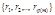(1). По св-вам ПрСВm 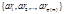(2)-то же ПрСВm. Следовательно, для каждого числа из (1) системы найдётся 1 и только 1 число из (2) системы, сравнимое с ним по mod m.

Φ(m) сравнений вида:

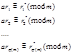
где 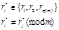i≠j

Перемножая это сравнение получаем: .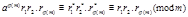

Т.к. r_i из ПрСВm, поэтому все они взаимно просты с модулем => 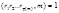. Поэтому можно обе части сравнения разделить на этот множитель. Получим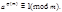

Частный случай теоремы (следствие). Малая т.Ферма.Если p- простое число и a не делится на p, то 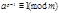. Замечание: если p-простое число и a не делится на p, то (a^p-1-1) нацело делится на p.

Т. Ферма используется в вопросах о выяснении того, будет ли число простым. Если число m: a^m-1 не сравнимо с 1 по mod m, то m-составное число - необходимое условие простоты. Если же 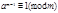. Если для m и a (a,m) ≡1(mod m), тогда m-псевдопростое.

Сущ.составные m , для кот. такое сравнение выполняется. Они наз.псевдопростыми.

Для всех (a,m) ≡1, 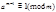, то m-кармайклово число. 1 кармайклово число-541.

Пример: m=18 a=5

5¹⁷≡ r(mod 18)

5¹⁷=(5²)⁸*5≡7⁸*5=(7²)⁴*5=(-5)⁴* =(5²)²*5≡7²*5=49*5≡-25≡11(mod 18)

Следствие из малой т.Ферма:a^p-1≡1 (mod p) 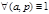,p-простое. Умножим обе части сравнения на а: a^p≡a (mod p). Такое сравнение верно, но для всех a€N и p-простых.

Применение теорем Эйлера и Ферма к вычислению остатков от деления

Задача: найти остаток от деления 3²⁰¹ на 7.По следствию из т.Ферма т.к.7-простое число и 3 не делится на 7=>3⁷≡3(mod 7)

3²⁰¹≡(3⁷)²⁸*3⁵≡3²⁸*3⁵≡3⁴*3⁵=8.

2 способ по т.Ферма: 3⁶≡1 (mod 7)

201/6=33 остаток 3

201=6*33+3. Возводим в 33 степень: (3⁶)³³≡1(mod 7). Домножим обе части сравнения на 3³.

3^6*33*3³≡3³(mod 7)

3²⁰¹≡27≡ =6 (mod 7)

Если n-составное, то пользуемся т.Эйлера.

2¹⁰¹⁹¹≡r (mod 33); (2,33)=1

По т.Эйлера 2^φ(33) ≡1(mod 33)

φ(33)=φ(3)*φ(11)=2*10=20 – верное сравнение

2²⁰ ≡1(mod33) (*)

10191=20*509+11

Обе части сравнения (*) возведем в степень 509.

(2²⁰)⁵⁰⁹≡1⁵⁰⁹≡1(mod 33). Умножим обе части на 2¹¹.

2¹⁰¹⁹¹≡2¹¹ (mod 33)

2¹¹=2⁵*2⁶=32*64=(-1)*(-2)≡2 (mod33)