Сравнения с неизвестными. Равносильные сравнения

Пусть , где а_i-целые числа. Т.е. f(x)-многочлен степени n. Тогда выражение вида f(x)=0 (mod m) (1)-сравнение от одной неизвестной переменной. Число x₀ наз. решением сравнения (1), если f(x₀)≡0(mod m) явл.верным числовым сравнением.

Пример.

1) 3x²+5x+1≡0 (mod 9)

х₀=1 – решение

3*1+5*1+1=9≡0(mod 9)

0-не решение, т.к. 1 не сравнимо с 0 по mod 9.

2: 3*4+5*2+1=23 не сравнимо с 0 по mod 9.

3: 3*9+5*3+1=43 не сравнимо с 0 по mod 9.

4: 3*16+5*4+1=69 не сравнимо с 0 по mod 9.

2,3,4-не решения.

Способы (м-ды) решения линейных сравнений (1 степени). Пусть ax≡b(mod m), где НОД (a,m)=1 имеет одно решение.

1 способ: перебор остатков.х:0,1,2,..,m-1.

Пример: 9x≡2(mod 10), (9,10)=1=>1 решение.

0: 9*0 не сравнимо с 2 по mod 10.

1: 9*1 не сравнимо с 2 по mod 10.

2: 9*2 не сравнимо с 2 по mod 10.

3: 9*3 не сравнимо с 2 по mod 10.

….

8:9*8≡2 (mod 10), x≡8(mod 10) -решение.

2 способ: преобразование.ax≡b(mod m). К правой части прибавляем число mt₀, такое, чтобы (b+ mt₀) делилось нацело на а.

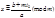
9x≡2(mod 10)

9x≡72(mod 10)

x≡8(mod 10)

2-10-10=-18

9x≡-18(mod 10)

x≡-2(mod 10)

x≡8(mod 10)

3 способ: формула Эйлера.Верна т.Эйлера (a,m)=1=>a^φ(m)≡1(mod m).

a*a^φ(m)-1≡a^φ(m)≡1(mod m)

a^φ(m)≡1(mod m) домножим на b.

a^φ(m)*b≡1*b(mod m) -верное сравнение.

a(a^φ(m)*b)≡b(mod m)-верное сравнение.

Решением сравнения ax≡b(mod m) явл. число a^φ(m)-1*b(mod m).

Пример:

Рассмотрим сравнение 27x≡18(mod 45)

(27,45)=9 и 18/9=>сравнение имеет 9 решений по теореме среди классов вычетов по mod 45.Разделим всё на 9.

1)3x≡2(mod 5)

3*4≡2(mod 5)

x≡4(mod 5) – 4 решения

2)Решаем сравнение по mod 45. x=4+5t.

3)Для t даём 9 значений t>=0 и t<=8. Получаем 9 решений.

4,9,14,19,24,29,34,39,44 (mod 45)-решения.