Использование критерия хи-квадрат для сравнения показателей внутри одной выборки

Критерий хи-квадрат может быть применен и для выявления сходства или различия внутри одной, но численно достаточно большой выборки. В этом случае вычленяются показатели (а их может быть два и больше), по которым и осуществляется сравне­ние. Этот аспект применения критерия xи-квадрат сближает его с коэффициентом корреляции, который также находит степень свя­зи между двумя или большим числом признаков. Различие между этими двумя методами, прежде всего в том, что для подсчета ко­эффициента корреляции необходимо знать все величины сравни­ваемых признаков, а для использования критерия хи-квадрат важ­но знать только уровни (градации) сравниваемых признаков.

При сравнении показателей с помощью критерия хи-квадрат нулевая гипотеза 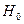звучит так: сравниваемые признаки не вли­яют друг на друга. В терминах корреляционных отношений: меж­ду признаками связи нет, корреляция не отличается от нуля.

Соответственно альтернативная гипотеза 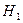звучит следую­щим образом: сравниваемые признаки влияют друг на друга. В терминах корреляционных отношений: между признаками связь есть, корреляция значимо отличается от нуля.

В этих случаях применение критерия хи-квадрат основывает­ся на использовании так называемых многопольных таблиц или, как их еще называют, таблиц сопряженности, т.е. таких таблиц, эмпирические данные в которых представлены размерностью большей, чем 2 x 2.

В этом случае расчет эмпирического значения критерия хи-квадрат может осуществляться по следующим двум формулам:

где 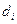разность между эмпирическими и «теоретическими» ча­стотами;

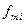есть вычисленная, или «теоретическая» частота.

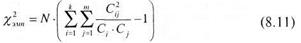
где k - число строк многопольной таблицы

т - число столбцов многопольной таблицы

N - общее число значений (элементов) в многопольной таблице, оно всегда является произведением N = k · т

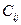- элементы многопольной таблицы

C_i - суммарные значения по строкам многопольной таблицы

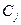- суммарные значения по столбцам многопольной таблицы

3адача 7. Влияет ли уровень интеллекта на профессиональ­ные достижения?

Решение. (Первый способ решения по формуле 8.10). Для решения этой задачи 90 человек оценили по сте­пени их профессиональных достижений и по уровню интеллекта. При разбиении на уровни (градации признака) по обоим признакам было взято три уровня. Для показателя профессиональ­ных достижений были получены следующие час­тоты признака: 20 человек с высоким уровнем профессиональных достижений, 40 со средним и 30 с низким. Первая группа составляет 22,2% вы­борки, вторая - 44,4% и третья — 33,3% от всей выборки. При разбиении по уровню интеллекта было взято три равных по численности группы, в каждой по 30 человек: уровень интеллекта ниже среднего, средний и выше среднего. В процентах каждая группа составляет 33,3% от всей выборки. Все эмпирические данные (частоты) представле­ны ниже в таблице 8.14:

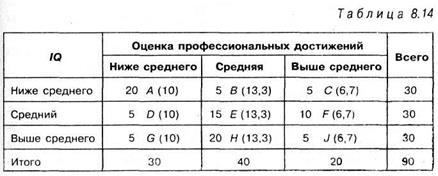
Для удобства каждая ячейка таблицы обозначена соответству­ющей латинской буквой: А, В, С ит.д. Таблица 8.14 устроена сле­дующим образом: в ячейку, обозначенную символом А, заносят­ся эмпирические частоты (или число) тех испытуемых, которые одновременно обладают следующей характеристикой: ниже среднего по уровню профессиональных достижений и ниже среднего по интеллекту. Таких испытуемых (эмпирических час­тот) оказалось 20. В ячейку, обозначаемую символом В, заносят­ся эмпирические частоты (или число) тех испытуемых, которые одновременно обладают характеристикой: средние по уровню профессиональных достижений и ниже среднего по интеллекту. Таких испытуемых (эмпирических частот) оказалось 5. В ячейку, обозначенную символом С, заносятся эмпирические частоты (или число) тех испытуемых, которые одновременно обладают характеристикой: выше среднего по уровню профессиональных достижений и ниже среднего по интеллекту. Таких испытуемых (эмпирических частот) оказалось также 5. Заметим, что 20 + 5 + 5 = 30, т.е. числу испытуемых, имеющих уровень интеллекта ниже среднего. Подобные «разбиения» были проделаны для каж­дой ячейки таблицы 8.14. Подчеркнем, что в круглых скобках в каждой ячейке таблицы представлены вычисленные для этой ячейки «теоретические» частоты.

Покажем, как для каждой ячейки таблицы 8.14 найти соот­ветствующую «теоретическую» частоту. Для каждого столбца таблицы подсчитываются так на­зываемые «частости» в процентах:

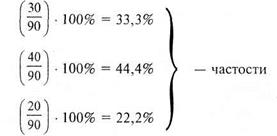
Полученные величины «частостей» дают возможность под­считать «теоретические» частоты для каждой ячейки таблицы 8.14. Они служат основой для подсчета «гипотетических» (а по сути теоретических) частот, т.е. таких частот, которые при за­данном соотношении экспериментальных данных должны были бы быть расположены в соответствующих ячейках таблицы 8.14. (Вспомним решение задачи 8.5).

Согласно этому положению «теоретическая» частота для ячейки А подсчитывается следующим образом. 30 человек имеют уровень интеллекта ниже среднего, поэтому 33,3% от этого чис­ла должны были бы попасть в группу с профессиональными до­стижениями ниже среднего уровня. Находим эту «гипотетичес­кую» величину так: .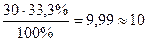

Аналогично «теоретическая» частота для ячейки D считается следующим образом: 30 человек имеют средний уровень интел­лекта, поэтому 33,3% от этого числа должны были бы попасть в группу с профессиональными достижениями среднего уровня. На­ходим эту «гипотетическую» величину так: .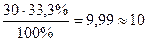

Аналогично «теоретическая» частота для ячейки G считается следующим образом: 30 человек имеют высокий уровень интел­лекта, поэтому 33,3% от этого числа должны были бы попасть в группу с профессиональными достижениями выше среднего уровня. Находим эту «гипотетическую» величину так: .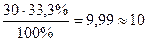

Рассмотрим, как производится подсчет для ячейки В: 30 че­ловек имеют низкий уровень интеллекта, поэтому 44,4% от это­го числа должны были бы попасть в группу с профессиональны­ми достижениями среднего уровня. Находим эту «гипотетичес­кую» величину так: .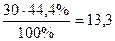

Аналогично, производится подсчет для ячейки Е: 30 человек имеют средний уровень интеллекта, поэтому 44,4% от этого чис­ла должны были бы попасть в группу с профессиональными до­стижениями среднего уровня. Находим эту «гипотетическую» ве­личину так: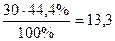

Аналогично, производится подсчет для ячейки Н: 30 человек имеют уровень интеллекта выше среднего, поэтому 44,4% от этого числа должны были бы попасть в группу с профессиональ­ными достижениями среднего уровня. Находим эту «гипотети­ческую» величину так: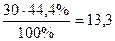

Рассмотрим, наконец, как производится подсчет для ячейки С: 30 человек имеют низкий уровень интеллекта, поэтому 22,2% от этого числа должны были бы попасть в группу с профессио­нальными достижениями выше среднего уровня. Находим эту «гипотетическую» величину так: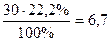

Расчет «теоретических гипотетических» частот для оставших­ся ячеек проведите самостоятельно.

Проверим правильность расчета «теоретических» частот для всех столбцов таблицы 8.14: 10 + 10 + 10 = 30; 13,3 + 13,3 + 13,3 = 39,9 ≈ 40; 6,7 + 6,7 + 6,7 = 20,1 ≈ 20.

Теперь все готово для использования формулы (8.1).

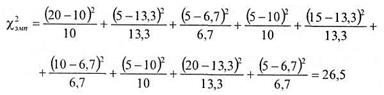
Для проверки правильности расчета «теоретических» частот в случае сравнения двух эмпирических наблюдений (см. раздел 8.2) или для сравнения показателей внутри одной выборки мо­жет использоваться следующая формула (8.12):

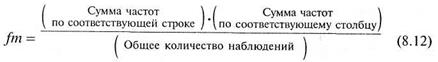
Проверим по этой формуле правильность наших расчетов:

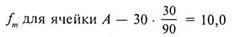
Число степеней свободы подсчитаем по знакомой формуле:v = (k - 1) · (с - 1) = (3 - 1) · (3 - 1) = 4, где k - число строк, а с - число столбцов и в соответствии с таблицей 12 Приложения 1 находим:

Полученные эмпирическая величина критерия хи-квадрат попала в зону значимости. Иными словами, следует принять гипотезу 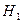о том, что уровень интеллекта влияет на успешность профессиональной деятельности.

Решение. (Второй способ решения по формуле 8.11).

Подставим данные таблицы 8.14 в формулу (8.11) получим:

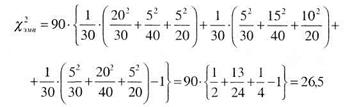
Как и следовало ожидать, эмпирическое значение xи-квадрат получено то же самое, что и при первом способе решения. Все дальнейшие операции уже проделаны выше при первом спосо­бе решения данной задачи, поэтому не будем их повторять. Бе­зусловно, что второй способ существенно проще первого, од­нако, при расчетах по формуле (8.11) можно легко допустить ошибки. Подчеркнем, что как первый, так и второй способы расчета эмпирического значения хи-квадрат позволяют работать с таблицами практически любой размерности: 3 х 4, 4 х 4, 5 х 3, 5 х 6 и т.п.