Критерий сравнения двух выборочных средних

Сравнение двух выборочных средних из нормальных совокупностей.

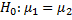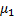Проверяется гипотеза , где – математическое ожидание первой генеральной совокупности, а 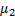– математическое ожидание второй генеральной совокупности.

Применение критерия сравнения двух выборочных средних при известных дисперсиях предусматривает вычисление статистики

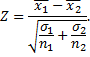
В случае принадлежности наблюдений нормальным законам статистика Z подчиняется стандартному нормальному закону. По таблице функции Лапласа необходимо найти критическую точку по равенству

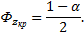
Если 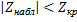, то нет оснований отвергнуть нулевую гипотезу 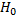о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями.

Сравнение двух средних нормальных совокупностей, дисперсии которых неизвестны и одинаковы.

По выборкам малого объема невозможно получить хорошие оценки генеральных дисперсий. В этом случае, если есть основания предположить, что генеральные дисперсии равны между собой, то можно воспользоваться критерием Стьюдента (сравнения средних).

Для того чтобы при заданном уровне значимости проверить нулевую гипотезу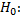

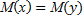
при конкурирующей гипотезе , следует вычислить наблюдаемое значение критерия

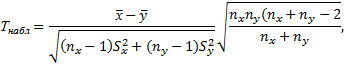
и по таблице критических точек распределения Стьюдента, по заданному уровню значимости и числу степеней свободы находят критическую точку .

Если 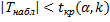, то отвергнуть нулевую гипотезу нет оснований.