Однофакторный дисперсионный анализ

Пусть генеральные совокупности распределены нормально и имеют одинаковую дисперсию, возможно неизвестную; математические ожидания также могут быть неизвестными и различными. Задача стоит следующая: при заданном уровне значимости по выборочным средним проверить нулевую гипотезу о равенстве всех математических ожиданий

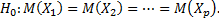
Иначе говоря, требуется установить, значимо или незначимо различаются выборочные средние.

Сравнивать попарно несколько средних нельзя, так как с возрастанием числа средних возрастает и наибольшее различие между ними. Среднее новой выборки может оказаться больше наибольшего или меньше наименьшего из средних, полученного до нового опыта. По этой причине для сравнения нескольких средних используют другой метод, который основан на сравнении дисперсий и назван дисперсионным анализом.

На практике дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние некоторый качественный фактор 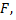который имеет 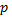уровней 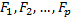на изучаемую величину 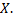Например, если требуется выяснить, какой вид удобрений наиболее эффективен для получения наибольшего урожая, то фактор 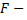удобрение, а его уровни – виды удобрений.

Основная идея дисперсионного анализа состоит в сравнении «факторной дисперсии», порождаемой воздействием фактора и «остаточной дисперсии», обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на 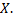В этом случае средние наблюдаемых значений на каждом уровне различаются также значимо.

Если установлено, что фактор существенно влияет на 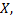а требуется выяснить, какой из уровней оказывает наибольшее воздействие, то дополнительно проводят попарное сравнение средних.

Иногда дисперсионный анализ применяется, чтобы установить однородность нескольких совокупностей. Однородные совокупности можно объединить в одну и тем самым получить о ней более полную информацию и более надежные выводы.

Пусть на количественный нормально распределенный признак воздействует фактор 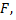который имеет 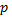уровней. Предполагаем, что число наблюдений на каждом уровне одинаково и равно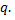

Пусть наблюдалось 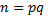значений признака 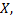где 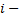номер испытания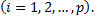

Результаты наблюдений приведены в таблице

Таблица 11

Номер испытания			…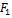
			…
			…
…	…	…	…	…
			…
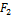
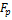
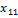
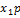
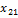
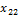
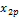
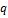
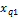
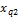
Групповая средняя			…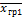

По определению, общая сумма квадратов отклонений групповых средних от общей средней

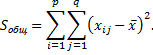
Факторная сумма квадратов отклонений групповых средних от общей средней, которая характеризует рассеяние между группами

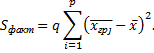
Остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней, которая характеризует рассеяние внутри группы

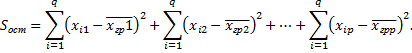
Практически остаточную сумму находят по равенству

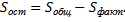
Убедимся, что 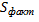характеризует воздействие фактора 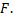Допустим, что фактор оказывает существенное влияние на 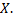Тогда группа наблюдаемых значений признака на одном определенном уровне отличается от групп наблюдений на других уровнях. Следовательно, различаются и групповые средние. Групповые средние тем больше рассеяны вокруг общей средней, чем большим окажется воздействие фактора. То есть для оценки воздействия фактора целесообразно составить сумму квадратов отклонений групповых средних от общей средней. Умножив эту сумму на 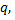получают 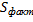, то есть 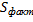характеризует воздействие фактора.

Убедимся, что отражает влияние случайных причин. Наблюдения одной группы не должно отличаться, но, поскольку на 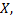кроме фактора 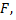воздействуют случайные причины наблюдения одной и той же группы различны, значит, рассеяны вокруг своей групповой средней. Таким образом, для оценки влияния случайных причин целесообразно составить сумму квадратов отклонений наблюдаемых значений каждой группы от своей групповой средней, то есть .

Убедимся, что 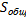отражает влияние и фактора и случайных причин. Рассмотрим все наблюдения как единую совокупность. Наблюдаемые значения признака различны вследствие воздействия фактора и случайных причин. Для оценки этого воздействия целесообразно составить сумму квадратов отклонений наблюдаемых значений от общей средней, то есть .

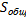Покажем, что

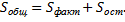
Ограничимся двумя уровнями 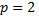и двумя испытаниями на каждом уровне 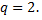Результаты испытаний заносятся в таблицу

Таблица 12

Номер испытания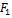

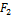
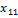
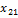
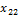
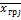
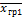
Тогда

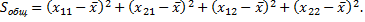
Вычтем и прибавим к каждому наблюдаемому значению на первом уровне групповую среднюю 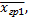а на втором уровне - 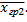Выполнив возведение в квадрат и учитывая, что сумма всех удвоенных произведений равна нулю, получим

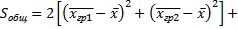
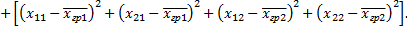
Итак,

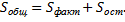
Вывод: нет надобности, непосредственно вычислять остаточную сумму, достаточно найти общую и факторную суммы, а затем их разность.

Разделив суммы квадратов отклонений на соответствующее число степеней свободы, получим общую, факторную и остаточную дисперсии

где 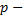число уровней фактора, 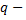число наблюдений на каждом уровне, число степеней свободы общей дисперсии, 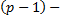число степеней свободы факторной дисперсии, 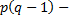число степеней свободы остаточной дисперсии.

Если нулевая гипотеза о равенстве средних справедлива, то все эти дисперсии являются несмещенными оценками генеральной совокупности. Например, учитывая, что объем выборки 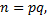можно записать

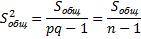
– исправленная выборочная дисперсия, которая является несмещенной оценкой генеральной дисперсии.

Итак, если стоит задача проверить при заданном уровне значимости нулевую гипотезу о равенстве нескольких средних нормальных совокупностей с неизвестными, но одинаковыми дисперсиями, то решение этой задачи сводится к сравнению факторной и остаточной дисперсий по критерию Фишера.

Пусть нулевая гипотеза о равенстве нескольких средних правильна. В этом случае факторная и остаточная дисперсии являются несмещенными оценками неизвестной генеральной дисперсии и, следовательно, различаются незначимо. Если сравнить эти оценки по критерию 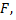то критерий укажет, что нулевую гипотезу о равенстве факторной и остаточной дисперсий следует принять.

Таким образом, если гипотеза о равенстве групповых средних правильна, то верна и гипотеза о равенстве факторной и остаточной дисперсий.

Пусть нулевая гипотеза о равенстве групповых средних ложна. В этом случае с возрастанием расхождения между групповыми средними увеличивается факторная дисперсия, а вместе с ней и отношение

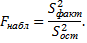
В итоге 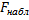окажется больше 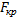и, следовательно, гипотеза о равенстве дисперсий будет отвергнута.

Таким образом, если гипотеза о равенстве групповых средних ложна, то ложна и гипотеза о равенстве факторной и остаточной дисперсий.

Вывод: для того чтобы проверить нулевую гипотезу о равенстве групповых средних нормальных совокупностей с одинаковыми дисперсиями, достаточно проверить по критерию 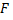нулевую гипотезу о равенстве факторной и остаточной дисперсий.

В этом и состоит метод дисперсионного анализа.