Корреляционная зависимость

Корреляционная зависимость – это зависимость, при которой изменение одной из величин влечет изменение среднего значения другой.

Пусть случайная величина Y – урожай зерна, а случайная величина X – количество внесенных удобрений. Функция Y не является функцией от X, так как с одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай. Но средний урожай является функцией от количества удобрений, т.е. Y связан с X корреляционной зависимостью.

Рассмотрим непрерывную двумерную случайную величину . Условной плотностью распределения составляющих X при данном значении Y=y называют отношение плотности совместного распределения 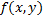системы к плотности распределения 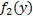составляющей Y

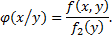
Аналогично определяется условная плотность составляющей Y при данном значении

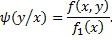
Вывод: умножая закон распределения одной из составляющих на условный закон распределения другой составляющей, найдем закон распределения системы случайных величин.

Важной характеристикой условного распределения вероятностей является условное математическое ожидание

,

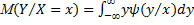где 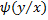– условная плотность случайной величины 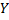при .

Условное математическое ожидание есть функция от , которую называют функцией регрессии Y на X. Аналогично определяется условное математическое ожидание случайной величины 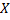и функции регрессии

.

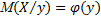Для описания системы двух случайных величин кроме математического ожидания используют такие характеристики, как корреляционный момент 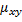и коэффициент корреляции .

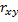Корреляционным моментом 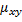случайных величин называют математическое ожидание произведения отклонений этих величин. Для вычисления корреляционного момента используют формулу

Корреляционный момент служит для характеристики связи между величинами . Корреляционный момент равен нулю, если независимы, т.е. если корреляционный момент не равен нулю, то – зависимые случайные величины.

Коэффициентом корреляции 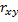случайных величин называют отношение корреляционного момента к произведению среднеквадратических отклонений этих величин

или

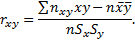
Коэффициент корреляции независимых случайных величин равен нулю. Коэффициент корреляции измеряет тесноту линейной связи между

Таким образом, две случайные величины называют коррелированными, если их корреляционный момент отличен от нуля .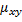

53.2. Линейная парная регрессия

Рассмотрим двумерную случайную величину , где – зависимые случайные величины. Одну из величин представляют как функцию другой. Так как точное приближение невозможно, то ограничиваются приближенным представлением величины Y в виде линейной функции величины X

.

Функцию называют среднеквадратической регрессией на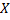

или

Коэффициент 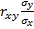называют коэффициентом регрессии Y на X, а уравнение прямой называют уравнением среднеквадратической регрессии Y на X.

Аналогично записывают уравнение прямой – среднеквадратической регрессии 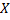на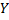

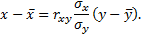
Обе прямые регрессии проходят через точку 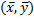, которую называют центром совместного распределения величин X и Y.