Двухфакторный дисперсионный анализ

Одной из используемых моделей данных в дисперсионном анализе является двухфакторная модель. Она состоит в учете систематических (первый фактор) и случайных (второй фактор) ошибок в определении измеряемых параметров.

Пусть с помощью методов 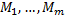производится измерение нескольких параметров, чьи точные значения - В таком случае, результаты измерений различных величин различными методами можно представить как

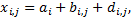
где 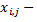результат измерения 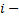го параметра по методу 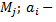точное значение 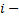го параметра; 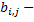систематическая ошибка измерения 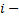го параметра по методу 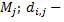случайная ошибка измерения 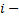го параметра по методу

Дисперсии случайных величин 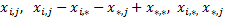где

выражаются

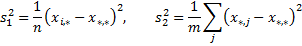
и удовлетворяют тождеству

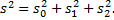
Двухфакторная схема позволяет лишь обнаружить систематические расхождения, но непригодна для их численной оценки с последующим исключением из результатов наблюдений. Эта цель может быть достигнута только при многократных измерениях, т.е. при повторных использованиях указанной схемы над данными повторных экспериментов.

Формулировка задачи может быть следующей. Пусть имеется выборка содержащая значений 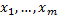некоторого показателя, измеренного в количественной шкале. Изучается влияние, которое оказывают на отклик два качественных признака – фактор 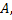который имеет 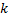уровней и фактор 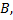разбитый на уровней 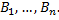Необходимо:

1) проверить гипотезу о принадлежности всех выборок одной генеральной совокупности, т.е. устанавливается, нельзя ли объяснить расхождение наблюдаемых значений для разных уровней факторов случайными обстоятельствами или влиянием неучтенных факторов;

2) если нулевая гипотеза отвергается, то оценить степень влияния каждого фактора;

3) выделить все пары групп, которые имеют между собой статистически значимые различия.

В рамках этой задачи типична ситуация, когда один из факторов, например 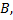является «мешающим», он включается в рассмотрение по той причине, что его влияние следует элиминировать, чтобы обнаружить и оценить индивидуальное влияние фактора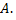

Общая методика анализа, как и в случае одного фактора, заключается в разложении общей вариации совокупности результатов наблюдения на частные вариации, обусловленные воздействием отдельных факторов и их комбинаций, и на остаточную вариацию, обусловленную случайными причинами. Оценка достоверности влияния факторов проводится по методу Фишера путем расчета отношения дисперсии, характеризующей статистическое колебание групповых средних по отдельным факторам, к дисперсии, характеризующей случайную вариацию.

Предположим, что измеряемая величина есть результат действия факторов и 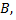составляющей 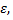которая является независимой, нормально распределенной случайной величиной

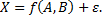
Принимается аддитивная и независимая модель действия факторов

Величины 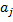и 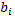называются вкладами факторов. Последние два условия всегда можно выполнить масштабированием величин 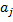и 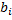за счет изменения величины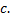

Для каждого наблюдения из рассматриваемой совокупности справедливо уравнение

Обычно наблюдения представляют структурной таблицей статистического комплекса. Приведем двухфакторный комплекс, в который каждому сочетанию 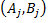уровней факторов, т.е. одной клетке таблицы, соответствует одно наблюдение. Сочетание символов 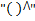обозначает статистическую оценку групповых средних.

Таблица 13

Фактор	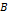Фактор	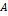Средние по строкам оценки вкладов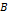
…	…	…
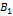
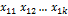
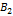
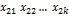
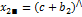
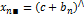
Средние по столбцам оценка вкладов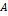

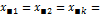
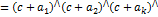
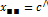
Оценки 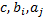могут быть получены с помощью метода наименьших квадратов минимизацией суммы

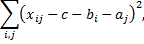
следовательно, минимум.

Основываясь на оценках метода наименьших квадратов

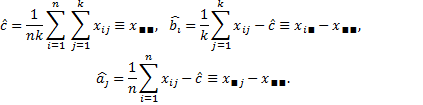
Введем обозначения для сумм квадратов отклонений под влиянием 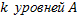и уровней фактора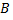

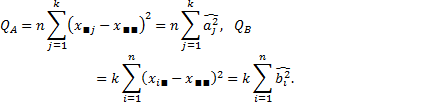
Введем обозначения для остаточной суммы квадратов

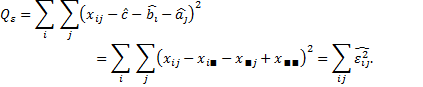
Введем обозначения для полной суммы квадратов наблюдений относительно общего среднего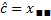

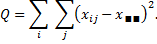
Тогда справедливо следующее соотношение

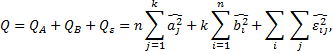
т.е. полная сумма квадратов отклонений является суммой квадратов вкладов по факторам и квадратов случайных отклонений. Другими словами, полное рассеяние есть сумма вариации под влиянием факторов и случайной составляющей.

Контрольные вопросы

1. С какой целью на практике применяют дисперсионный анализ?

2. В чем состоит метод дисперсионного анализа?

3. В чем отличие между однофакторной и двухфакторной моделью?

4. Что позволяет обнаружить двухфакторная схема?