Понятие о нелинейной регрессии

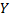Пусть данные наблюдений над количественными признаками сведены в корреляционную таблицу. Тем самым можно считать, что наблюдаемые значения разбиты на группы, причем, каждая группа содержит те значения 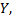которые соответствуют определенному значению 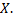Например, дана корреляционная таблица

Таблица 14

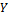
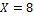
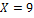
3	4	13
5	6	7
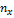
	10	20
	4,2	3,7

Условные средние можно назвать групповыми средними. Групповая средняя первой группы

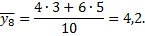
Групповая средняя второй группы

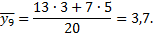
Принимая во внимание, что все значения признака 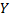разбиты на группы, можно представить общую дисперсию признака в виде суммы внутригрупповой и межгрупповой дисперсий

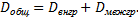
Если 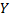связан с функциональной зависимостью, то определенному значению соответствует одно значение 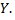В этом случае в каждой группе содержаться равные между собой значения 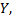поэтому групповая дисперсия каждой группы равна нулю. Следовательно, средняя арифметическая групповых дисперсий, т.е. внутригрупповая дисперсия 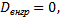тогда

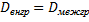
или

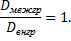
Если 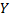связан с корреляционной зависимостью, то определенному значению соответствуют различные значения 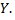В этом случае групповая дисперсия каждой группы отлична от нуля. Следовательно средняя арифметическая групповых дисперсий 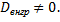Тогда

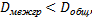
отсюда

Вывод: чем ближе связь между признаками к функциональной, тем меньше , следовательно, тем больше приближается 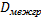к 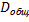и отношение 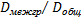- к единице.

Таким образом, целесообразно рассматривать в качестве меры тесноты корреляционной зависимости отношение межгрупповой дисперсии к общей.