Ранговая корреляция

Допустим, что объекты генеральной совокупности обладают двумя качественными признаками. Под качественным подразумевается признак, который невозможно измерить точно, но он позволяет сравнивать объекты между собой и, следовательно, расположить их в порядке убывания или возрастания качества. Пусть выборка объема содержит независимые объекты, которые обладают двумя качественными признаками и 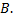Для оценки степени связи признаков вводят коэффициенты ранговой корреляции Спирмена и Кендалла.

Для практических целей использование ранговой корреляции весьма полезно. Например, если установлена высокая ранговая корреляция между двумя качественными признаками изделий, то достаточно контролировать изделия только по одному из признаков, что удешевляет и ускоряет контроль.

Итак, проблема оценки тесноты связи разрешима, если упорядочить, или ранжировать, объекты анализа по степени выраженности измеряемых признаков. При этом каждому объекту присваивается определенный номер, называемый рангом. Например, объекту с наименьшим проявлением признака присваивается ранг 1 и так далее. Если объекты ранжированы по двум признакам, то имеется возможность оценить тесноту связи между признаками, основываясь на рангах, т.е. тесноту ранговой корреляции.

Коэффициент ранговой корреляции Спирмена находится по формуле

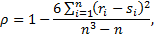
где 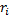и 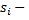ранги i-го объекта по переменным и 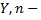число пар наблюдений.

Если между двумя качественными признаками имеется полная прямая зависимость, т.е. ранги объектов совпадают при всех значениях 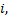то выборочный коэффициент ранговой корреляции Спирмена равен единице

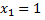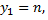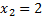Если между двумя качественными признаками имеется противоположная зависимость, т.е. рангу соответствует ранг рангу соответствует ранг 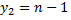и т.д., то коэффициент ранговой корреляции Спирмена равен минус единице

Если между двумя качественными признаками нет ни полной прямой зависимости, ни противоположной зависимости, то коэффициент Спирмена заключен между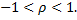

При ранжировании иногда невозможно найти существенные различия между объектами по величине проявления рассматриваемого признака. Объекты оказываются связанными. Связанным объектам приписывают одинаковые средние ранги, такие, чтобы сумма всех рангов оставалась такой же, как и при отсутствии связанных рангов. Например, если четыре объекта оказались равнозначными в отношении рассматриваемого признака и невозможно определить, какие из четырех рангов (4, 5, 6, 7) приписать этим объектам, то каждому объекту приписывается средний ранг, равный

При наличии связанных рангов ранговый коэффициент корреляции Спирмена вычисляется по формуле

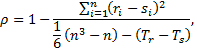
где

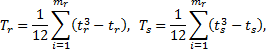
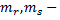число групп неразличимых рангов у переменных и 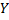, 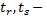число рангов, входящих в группу неразличимых рангов переменных и

Для того чтобы при уровне значимости проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена при конкурирующей гипотезе о неравенстве нулю коэффициента, нужно вычислить критическую точку

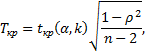
где 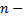объем выборки, 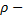выборочный коэффициент ранговой корреляции Спирмена, 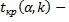критическая точка двусторонней критической области, которую находят по таблице критических точек Стьюдента, по уровню значимости и числу степеней свободы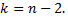

Если 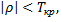то нет оснований отвергать нулевую гипотезу. Ранговая корреляционная связь между качественными признаками незначима.

Если 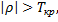то нулевую гипотезу отвергают. Между качественными признаками существует значимая ранговая корреляционная связь.

Контрольные вопросы

1. Что целесообразно рассматривать в качестве меры тесноты корреляционной зависимости?

2. Что называют межгрупповой дисперсией?

3. В каком случае корреляцию называют криволинейной?

4. Какие задачи решает теория криволинейной корреляции?