Корреляция.

Предположим, что проведена серия опытов в результате которых каждый раз наблюдается двумерная случайная величина .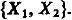

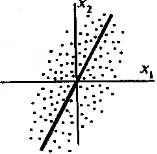
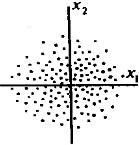
Может оказаться. Что изображающие точки в среднем располагаются вдоль некоторой прямой, так, что 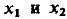имеют чаще всего одинаковый знак, это наводит на мысль, что между 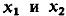имеется статическая связь – называемая корреляцией. Если значения расположены – хаотично , то говорят, что величины некоррелированные т.е. у них нет устойчивой связи в вероятном смысле. Качественной характеристикой степени статической связи служит их ковариационный момент 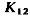или корреляционный момент 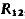,определяемый как среднее значение произведения :

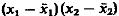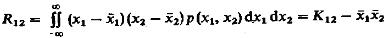(8) иногда вводят безразмерный коэффициент корреляции:

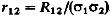(9) если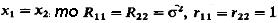

Если размерность случайного вектора больше двух, то можно построить всевозможные перекрестные корреляционные моменты

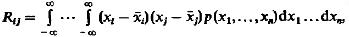(11)

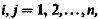
И коэффициент корреляции :

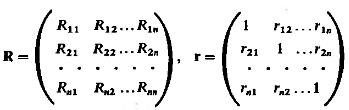(12) (13)

Случайные величины 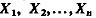статически независимы.

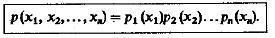(14)