Занятие №3. Формулы Крамера. Матричный способ решения систем линейных алгебраических уравнений. Решение систем линейных алгебраических уравнений методом Гаусса
№1. Решить систему линейных алгебраических уравнений методом Крамера:
а) 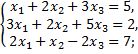 б)
б) 
в)  г)
г) 
№2. Вычислить систему матричным способом:
а) 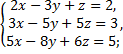 б)
б) 
в) 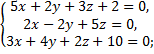 г)
г) 
№3. Решить уравнение:
а) 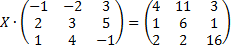 ;
;
б) 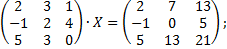
в)  .
.
№4. Решить систему линейных алгебраических уравнений методом Гаусса:
а)  б)
б) 
в)  г)
г) 
Занятие №4. Критерий Кронекера-Капелли совместности систем линейных алгебраических уравнений. Общее, базисное, частные решения. Однородные системы линейных алгебраических уравнений
№1. Исследовать систему уравнений с помощью теоремы Кронекера-Капелли:
а) 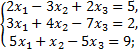
б) 
в) 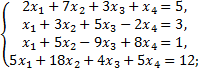
г) 
№2. Найти базисные решения системы уравнений:
а) 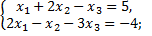
б) 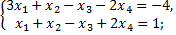
в) 
№3. Решить систему уравнений:
а) 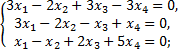
б) 
в) 
Занятие №5. Векторы. Основные понятия
№1. Найти координаты вектора 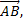 если:
если:
а) 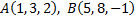 б)
б) 
в)  г)
г) 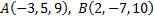
№2. Найти проекции вектора  , если
, если
а)  ;
;
б) 
№3. Найти длину вектора:
а) 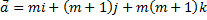 ;
;
б) 
в) 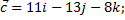
г) 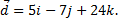
№4. Даны радиус-векторы вершин треугольника 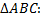
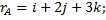


показать, что треугольник равносторонний.
№5. Даны точки 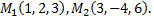 Найти длину и направление вектора
Найти длину и направление вектора 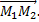
№6. Вычислить модуль вектора

и найти направляющие косинусы.
№7. Дан вектор 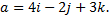 Найти вектор
Найти вектор 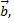 если
если 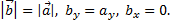
№8. Нормировать вектор 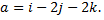
№9. Разложить вектор 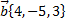 по базису
по базису
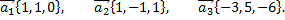
Примечание: 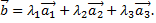
№10. Вектор 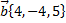 заданный в векторов
заданный в векторов 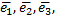 выразить в базисе
выразить в базисе 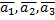

Примечание: связь между базисами
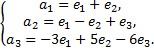
Матрица перехода к новому базису
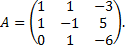
Координаты вектора 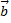 в новом базисе
в новом базисе
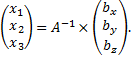
№11. Показать, что векторы образуют базис

Примечание: составляют и решают матричное уравнение, если решение единственное 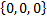 , то векторы линейно независимы
, то векторы линейно независимы

№12. Выяснить вопрос о линейной независимости векторов
а) 
б) 
Дата добавления: 2015-08-11; просмотров: 892;
