Занятие №8. Линии второго порядка
№1. Определить координаты центра и радиус окружности
а) 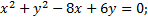
б) 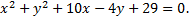
№2. Составить уравнение окружности, проходящей через точки  если ее центр лежит на прямой
если ее центр лежит на прямой
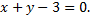
№3. Составить уравнение окружности, проходящей через точки 
№4. Составить уравнение эллипса, проходящего через точки
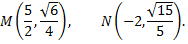
№5. Найти длину перпендикуляра восстановленного из первого фокуса эллипса
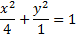
большой оси до пересечения с эллипсом.
Примечание:

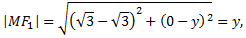
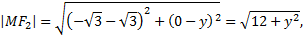

№6. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса

Примечание:


№7. Составить уравнение эллипса, если известно, что  и
и 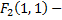 фокусы этого эллипса, а длина большой оси равна 2.
фокусы этого эллипса, а длина большой оси равна 2.
Примечание:

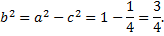
Центр эллипса
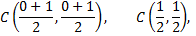
следовательно,
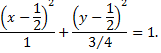
№8. Составить уравнение гиперболы, проходящей через точку  , если асимптоты гиперболы имеют уравнения
, если асимптоты гиперболы имеют уравнения
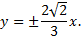
№9. Составить уравнение гиперболы, если ее эксцентриситет равен 2 и фокусы совпадают с фокусами эллипса

Примечание:
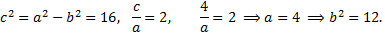
№10. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси 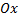 и отсекающей от прямой
и отсекающей от прямой 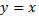 хорду длиной
хорду длиной 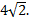
Примечание: обозначим хорду 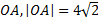

Так как точка  лежит на прямой
лежит на прямой  тогда
тогда
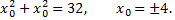
Точка 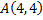 или
или  принадлежит параболе
принадлежит параболе 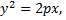 следовательно,
следовательно, 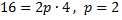 или
или
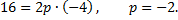
Уравнение параболы может быть

№11. На параболе 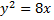 найти точку, расстояние которой от директрисы равно 4.
найти точку, расстояние которой от директрисы равно 4.
Примечание:
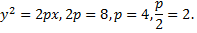
Пусть 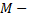 произвольная точка на параболе,
произвольная точка на параболе,  точка симметричная точки
точка симметричная точки 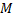 относительно
относительно 
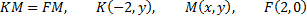

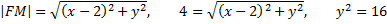
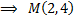 или
или 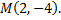
Дата добавления: 2015-08-11; просмотров: 2173;
