Занятие №10. Плоскость
№1. Уравнение плоскости 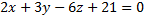 привести к нормальному виду.
привести к нормальному виду.
Примечание:
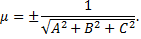
№2. Определить расстояние от точки 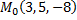 до плоскости
до плоскости 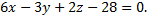
Примечание:
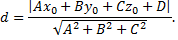
№3. Составить уравнение плоскости, проходящей через точку 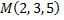 и перпендикулярной вектору
и перпендикулярной вектору 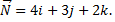
№4. Составить уравнение плоскости, проходящей через точку 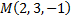 параллельно плоскости
параллельно плоскости 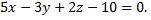
№5. Из точки 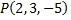 на координатные оси опущены перпендикуляры. Составить уравнение плоскости, проходящей через их основания.
на координатные оси опущены перпендикуляры. Составить уравнение плоскости, проходящей через их основания.
Примечание: необходимо записать уравнение плоскости, проходящей через три точки
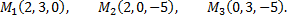
№6. Составить уравнение плоскости, проходящей через линию пересечения плоскостей

и точку 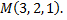
Примечание: записать уравнение пучка плоскостей
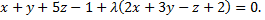
Так как точка 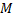 лежит на искомой плоскости, то ее координаты должны удовлетворять этому уравнению, откуда
лежит на искомой плоскости, то ее координаты должны удовлетворять этому уравнению, откуда 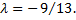
Подставив значение  в уравнение пучка плоскостей, найдем искомой уравнение плоскости.
в уравнение пучка плоскостей, найдем искомой уравнение плоскости.
№7. Составить уравнение плоскости, проходящей через точки 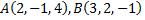 перпендикулярно плоскости
перпендикулярно плоскости
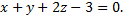
Примечание: следует найти векторное произведение векторов  и
и 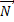 -нормального вектора плоскости
-нормального вектора плоскости
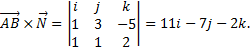
Следовательно,
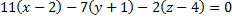
или
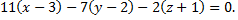
№8. Найти уравнение плоскости, проходящей через точку 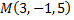 и перпендикулярной плоскостям
и перпендикулярной плоскостям

Примечание: следует найти векторное произведение нормальных векторов плоскостей

тогда
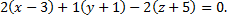
Дата добавления: 2015-08-11; просмотров: 1754;
