Занятие №11. Прямая в пространстве

№1. Уравнение прямой привести к каноническому виду

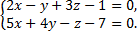
Примечание: следует найти вектор, параллельный искомой прямой, он должен быть перпендикулярен нормальным векторам плоскостей, на пересечение которых получилась прямая

Общее уравнение прямой в каноническом виде имеет вид

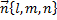– направляющий вектор прямой. В нашем случае

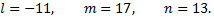
Затем находят координаты точки, принадлежащей данной прямой. Пусть тогда

Таким образом, можно записать искомое уравнение прямой

№2. Составить уравнение прямой, проходящей через точку параллельно вектору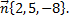

№3. Составить уравнение прямой, проходящей через точку перпендикулярно векторам

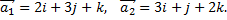
Примечание: следует найти направляющий вектор прямой

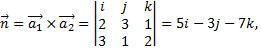
тогда

№4. Привести к каноническому виду уравнение прямой

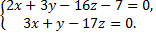
Примечание: следует найти координаты точки, принадлежащей данной прямой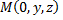

Определяют направляющий вектор прямой

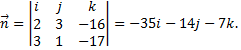
Искомое уравнение прямой

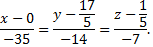
№5. Найти уравнение прямой, проходящей через и параллельно прямой

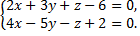
№6. Записать параметрическое уравнение прямой, проходящей через точки и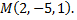

Примечание: следует записать каноническое уравнение прямой, проходящей через две заданные точки, а затем перейти к параметрическому

№7. Найти точку пересечения прямой

и плоскости

Примечание: от канонического уравнения прямой следует перейти к параметрическому, затем переменные выраженные через параметр, подставить в уравнение плоскости, найти параметр и вернуться к параметрическому уравнению прямой, чтобы, зная параметр, найти искомые координаты точки.

№8. Вычислить расстояние между двумя параллельными прямыми

Примечание: найти координаты любой точки, принадлежащей одной из прямых

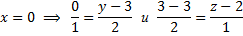
решая, получим

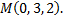
Найти расстояние от точки 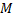до прямой

№9. Составить уравнение прямой, проходящей через точку перпендикулярно плоскости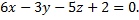

№10. Составить уравнение плоскости, проходящей через точку перпендикулярно прямой

Примечание: определить координаты точки, принадлежащей заданной прямой

точка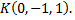

Следует определить координаты нормального вектора плоскости, как результат векторного произведения нормальных векторов плоскостей, на пересечение которых задана прямая

Искомое уравнение плоскости

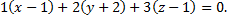
№11. При каком значении прямая

параллельна плоскости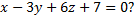

Примечание: прямая параллельна плоскости, если ее направляющий вектор перпендикулярен нормальному вектору плоскости