аксонометрическая и вторичная проекции точки вполне определяют её положение в пространстве.
Аксонометрические проекции обратимы, если известна аксонометрия трех главных направлений измерений фигуры и коэффициенты искажения по этим направлениям.
Аксонометрические проекции фигуры являются её проекциями на плоскости произвольного положения при произвольно выбранном направлении проецирования.
Очевидно возможно и обратное. На плоскости можно выбрать произвольное положение осей с произвольными аксонометрическими масштабами.
В пространстве всегда возможно такое положение натуральной системы прямоугольных координат и такой размер натурального масштаба по осям, параллельной проекцией которых является данная аксонометрическая система.
Немецкий ученый Карл Польке (1810-1876) сформулировал основную теорему аксонометрии: три отрезка прямых произвольной длины, лежащих в одной плоскости и выходящих из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на координатных осях от начала.
Согласно этой теореме, любые три прямые в плоскости, исходящие из одной точки и не совпадающие между собой, можно принять за аксонометрические оси. Любые отрезки произвольной длинны на этих прямых, отложенные от точки их пересечения, можно принять за аксонометрические масштабы. Эта система аксонометрических осей и масштабов является параллельной проекцией некоторой прямоугольной системы координатных осей и натуральных масштабов.
В практике построения аксонометрических изображений обычно применяют лишь некоторые определенные комбинации направлений аксонометрических осей и аксонометрических масштабов: прямоугольная изометрия и диметрия, косоугольная фронтальная диметрия, кабинетная проекция и др.
| Стандартные аксонометрические проекции |
Согласно ГОСТ 2.317-69, из прямоугольных аксонометрических проекций рекомендуется применять прямоугольные изометрию и диметрию.

| Между коэффициентами искажения и углом φ, образованным направлением проецирования и картинной плоскостью, существует следующая зависимость: u2+υ2+ω2=2+ctq2φ, еслиφ=90o, то u2+υ2+ω2=2, В изометрии u=υ=ωи, следовательно, 3u2=2,откудаu=Ö2/3 ≈ 0,82. Таким образом, в прямоугольной изометрии размеры предмета по всем трем измерениям сокращаются на 18 %. ГОСТ рекомендует изометрическую проекцию строить без сокращения по осям координат (рис.9.2), что соответствует увеличению изображения против оригинала в 1,22 раза. |
| Рисунок 9.2. Расположение осей в изометрии |
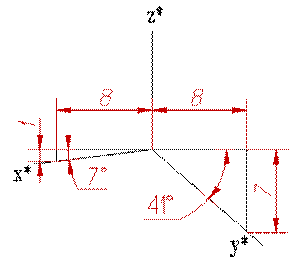
| При построении прямоугольной диметрической проекции сокращение длин по оси y'(рис.9.3)принимают вдвое больше, чем по двум другим, т.е. полагают, что u=ω, а υ=0,5u. Тогда 2u2+(0,5u)2=2, откуда u2=8/9 и u≈0,94, а υ=0,47. В практических построениях от таких дробных коэффициентов обычно отказываются, вводя масштаб увеличения, определяемый соотношением 1/0,94=1,06, и тогда коэффициенты искажения по осям x' и z' равны единице, а по оси y' вдвое меньше υ=0,5. Из косоугольных аксонометрических проекций ГОСТом предусмотрено применение фронтальной и горизонтальной изометрии и фронтальной диметрии (последнюю ещё называют кабинетной проекцией). |
| Рисунок 9.3. Расположение осей в диметрии |
| Окружность в аксонометрии |
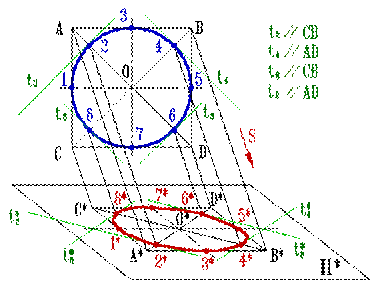
| При параллельном проецировании окружности на какую-нибудь плоскость П* получаем ее изображение в общем случае в виде эллипса (рис. 9.4). Как бы ни была расположена плоскость окружности, сначала целесообразно построить параллелограмм A*B*C*D* – параллельную проекцию квадрата ABCD, описанного около данной окружности, а затем с помощью восьми точек и восьми касательных вписать в него эллипс. Точки 1, 3, 5 и 7 – середины сторон параллелограмма. Точки 2, 4, 6 и 8 расположены на диагоналях так, что каждая из них делит полудиагональ в соотношении 3:7. Действительно, на основании свойств параллельного проецирования можно записать, что А2/1О=A*2*/2*O*, Но А1/1О=(r√2-r)/r≈3/7. Из восьми касательных к эллипсу первые четыре – это стороны параллелограмма, а остальные t2, t4, t6 иt8– прямые, параллельные его диагоналям. Так касательнаяt2* к эллипсу параллельна диагонали C*D*, Объясняется это тем, что t2* и C*D* являются проекциями двух параллельных прямых t2 и CD. | |
| Рисунок 9.4. Проецирование окружности на плоскость | ||
Графические построения, предшествующие вычерчиванию самого эллипса, целесообразно выполнять в следующей последовательности (рис.9.5):
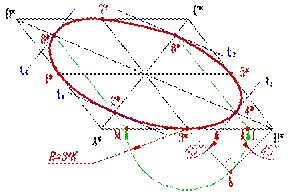
| 1. Построить аксонометрическую проекцию квадрата - параллелограмм A*B*C*D* и провести диагонали A*C* и B*D*; 2. Отметить середины сторон параллелограмма – точки 1*, 3*, 5* и 7* ; 3. На отрезке 3*B*, как на гипотенузе, построить прямоугольный равнобедренный треугольник 3*KB*; 4. Из точки 3* радиусом 3*K описать полуокружность, которая пересечет A*B* в точках L и M; эти точки делят отрезок 3*A* и равный ему отрезок 3*B* в отношении 3:7 ; 5. Через точки L и М провести прямые параллельные боковым сторонам параллелограмма, и отметить точки 2*, 4*, 6* и 8* расположенные на диагоналях; 6. Построить касательные к эллипсу в найденных точках. Касательныхt2 и t6 параллельны BD, а касательных t4 и t8 параллельны AC. 7. Получив восемь точек и столько же касательных, можно с достаточной точностью вычертить эллипс. | |

| Рисунок 9.5. Построение эллипса | |
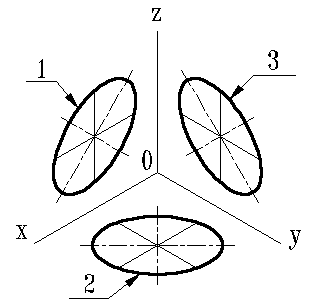
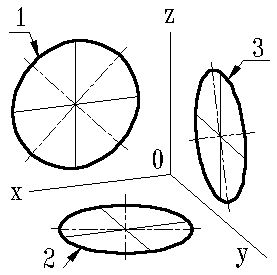
ГОСТ 2.317-69 определяет положение окружностей, лежащих в плоскостях, параллельных плоскостям проекций для прямоугольной изометрической проекции (рис.9.6) и для прямоугольной диметрии (рис.9.7).
| 
|
| Рисунок 9.6. Изометрические проекции окружностей, расположенных в плоскостях параллельных плоскостям проекций | Рисунок 9.7. Диметрические проекции окружностей, расположенных в плоскостях параллельных плоскостям проекций |
Если изометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1,2, 3 равна 1,22, а малая ось -0.71 диаметра окружности.
Если изометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось ось эллипсов 1, 2, 3 равна диаметру окружности, а малая - 0.58 диаметра окружности.
Если димметрическую проекцию выполняют без искажения по осям x и z то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 - 0.95, эллипсов 2 и 3 - 0.35 диаметра окружности.
Если диметрическую проекцию выполняют с искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 - 0.9, эллипсов 2 и 3 - 0,33 диаметра окружности.
1-эллипс (большая ось расположена под углом 900 к оси y); 2-эллипс (большая ось расположена под углом 900 к оси z); 3-эллипс (большая ось расположена под углом 900 к оси x).
| Построение аксонометрических изображений |
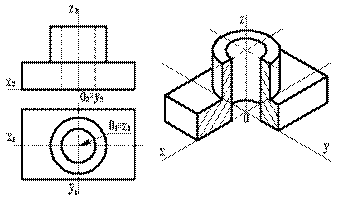
| Переход от ортогональных проекций предмета к аксонометрическому изображению рекомендуется осуществлять в такой последовательности (рис. 9.8): 1. На ортогональном чертеже размечают оси прямоугольной системы координат, к которой и относят данный предмет. Оси ориентируют так, чтобы они допускали удобное измерение координат точек предмета. Например, при построении аксонометрии тела вращения одну из координатных осей целесообразно совместить с осью тела. 2. Строят аксонометрические оси с таким расчетом, чтобы обеспечить наилучшую наглядность изображения и видимость тех или иных точек предмета. 3. По одной из ортогональных проекций предмета чертят вторичную проекцию. 4. Создают аксонометрическое изображение, для наглядности делают вырез четверти. | |
| Рисунок 9.8. Построение аксонометрического изображения | ||
ГОСТ 2.317-69 определяет условности и способы нанесения размеров при построении аксонометрического изображения, основное внимание следует обратить на следующих:
| 
|
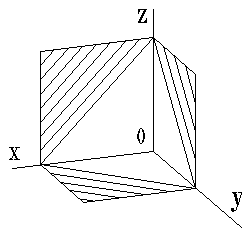
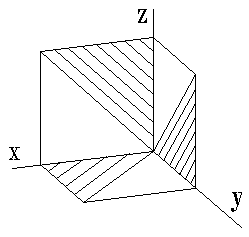
| Рисунок 14.9 Штриховка в аксонометрии |
·Линии штриховки сечения в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям.
·При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии – параллельно измеряемому отрезку.
· В аксонометрических проекциях спицы маховиков и шкивов, ребра жесткости и подобные элементы штрихуют.
Дата добавления: 2015-08-14; просмотров: 3066;
