В основу классификации кривых положена природа их уравнений.

Кривые подразделяются на алгебраические и трансцендентные в зависимости от того, являются ли их уравнения алгебраическими или трансцендентными в прямоугольной системе координат.

Плоская кривая линия называется алгебраической, если её уравнение f (xy)=0. Функция f (xy)является степенным множителем относительно переменных хи у; в остальных случаях кривая называется трансцендентной.

Кривая линия, представленная в декартовых координатах уравнением п- й степени, называется алгебраической кривой п-го порядка.

Порядок плоской алгебраической кривой линии определяется наибольшим числом точек её пересечения прямой линией. Любая прямая линия может пересекать алгебраическую кривую линию п-го порядка не более чем в п точках.

Рассмотрим несколько примеров алгебраической кривой линии:

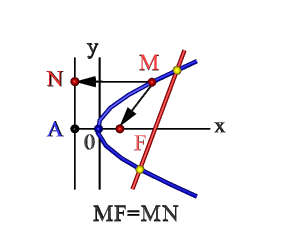Рисунок 7.2. Парабола	1. Парабола – кривая второго порядка, прямая пересекает ее в двух точках (рис.7.2). При этом парабола может быть определена как: -множество точек М(xy) плоскости, расстояние FM которых до определенной точки F этой плоскости (фокуса параболы) равно расстоянию MN до определенной прямой АN - директрисы параболы; -линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и параллельная какой либо касательной плоскости этого конуса; -в прямоугольной системе координат 0ху с началом в вершине параболы и осью 0х направленной по оси параболы уравнение параболы имеет так называемый канонический вид y2=2px, где р (фокальный параметр) - расстояние от фокуса до директрисы. 2. Гипербола : - множество точек М плоскости (рис.7.3) разность (по абсолютной величине) расстояний F1M и F2Mкоторых до двух определенных точек F1 и F2 этой плоскости (фокусов гиперболы) постоянна: F1M - F2M=2а<2с Середина 0 отрезка F1F2(фокусного расстояния) называется центром гиперболы; - линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающая обе его полости; - в прямоугольной системе координат 0ху с началом в центре гиперболы, на оси 0х которой лежат фокусы гиперболы уравнение гиперболы имеет так называемый канонический х2/а2 - у2/в2=1, в2=с2 - а2, где а и в длинны полуосей гиперболы. 3. Эллипс : - множество точек М плоскости (рис.7.4), сумма расстояний МF1 и МF2 которых до двух определенных точек F1 и F2 (фокусов эллипса) постоянна МF1+МF2=2а. Середина0отрезка F1F2 (фокусного расстояния)называется центром эллипса; - линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающей все прямолинейные образующие одной полости этого конуса; - в прямоугольной системе координат 0ху с началом в центре эллипса, на оси 0х которой лежат фокусы эллипса уравнение эллипса имеет следующий вид х2/а2+у2/в2=1, где а и в - длинны большой и малой полуосей эллипса. При а=в фокусы F1 и F2 совпадают и указанное уравнение определяет окружность, которая рассматривается как частный случай эллипса. Рассмотренные плоские кривые линии, получаемые при пересечении поверхности прямого кругового конуса плоскостями, различно расположенными по отношению к оси конуса, называют кривыми конических сечений.
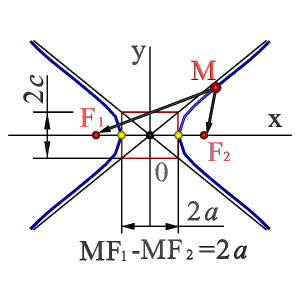Рисунок 8.3. Гипербола
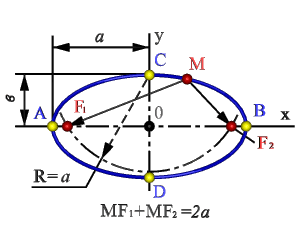Рисунок 7.4. Эллипс
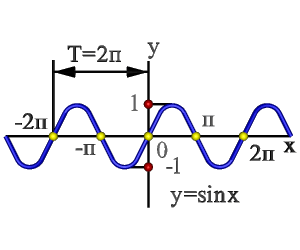Рисунок 7.5. Синусоида

Трансцендентные кривые в отличие от алгебраических могут иметь бесконечное количество точек пересечения с прямой, точек перегиба, вершин и т.п.

Синусоида - трансцендентная плоская кривая линия (рис.7.5), получающаяся в результате двойного равномерного движения точки - поступательного и возвратно-поступательного в направлении, перпендикулярном первому.

Синусоида - график функции у=sin x, непрерывная кривая линия с периодом Т=2п.

Наряду с этим у трансцендентных кривых могут быть характерные точки, которых не существует у алгебраических кривых: точки прекращения, угловые точки (точки излома), асимптотические точки. Простейшими примерами трансцендентных кривых служат графики функций логарифмической, показательной тригонометрической, а также все спирали, циклоиды и т.п.

Кривая линия как траектория движущейся точки должна быть непрерывной. Движущаяся точка в любом положении должна иметь определенное направление движения. Это направление указывает прямая (касательная), проходящая через рассматриваемую точку.

Длина отрезка кривой линии определяется в общем случае, как сумма длин отрезков вписанной в нее ломаной линии, с заданной точностью передающей форму кривой.

Особый интерес представляют окружность и цилиндрическая винтовая линии, каждая из которых является эталоном соответственно плоских и пространственных кривых линий.

В практике конструирования линий и поверхностей широко используются обводы. Это кривые, составленные из дуг различных кривых, определенных парами смежных точек. Обводом ряда точек плоскости является плоская кривая, пространства - пространственная. Точки стыка дуг называются узлами. Обвод заданный координатами своих точек называется дискретным. Обвод называется гладким, если дуги обвода в узлах имеют общие касательные.

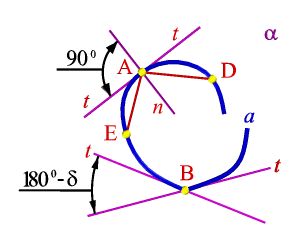Рисунок 7.6. Касательные к кривой линии

Плоская кривая а построена в плоскости a (рис.7.6). Через точку А проведены секущие хорды АЕ и АD. Если точку Еприближать к точке А, секущая АЕповорачивается вокруг точки А. Когда точка Е совпадет с точкой А (А≡Е) секущая АЕдостигнет своего предельного положения t.В этом предельном положении секущая называется полукасательной к кривой а в точке А. Секущая АD в предельном положении А≡D также представлена полукасательной t. Кривая линия в точке А имеет две полукасательные прямые, которые совпадают и определяют одну касательную к кривой линии в точке А – кривая в этой точке называется плавной. Кривая плавная во всех её точках называется плавной кривой линией. Нормалью п в точке А кривой линии называется перпендикуляр к касательной.

На кривой линии могут быть точки где разнонаправленные полукасательные не принадлежат одной прямой, а составляют между собой угол. Так на кривой а в точке В угол δмежду полукасательными не равен 180⁰. Точка В в этом случае называется точкой излома или выпадающей точкой.

Рисунок 7.7. Кривая линия как траектория движения точки

Плоскую кривую линию можно рассматривать как траекторию движения точки в плоскости (рис.8.7); точка движется по касательной к кривой линии, обкатывая эту кривую без скольжения. Движение точки вдоль кривой а связано с непрерывным изменением двух величин: расстояния S, на которое удалена точка от начального положения и угла α поворота касательной относительно начального положения. Если с увеличением пути S непрерывно увеличивается и α, кривая называется простой. Угол α (угол смежности) между касательными в двух бесконечно близких точках кривой, отнесенный к длине дуги между этими точками, определяет степень искривленности кривой линии, т.е. определяет кривизнукривой.

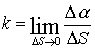
, предел отношения угла смежности касательных к соответствующей дуге.

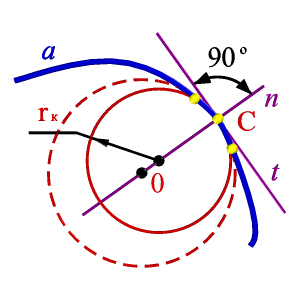Рисунок 7.8. Кривизна кривой

Кривизна прямой в любой её точке равна нулю. Кривизна произвольной кривой линии в различных точках различна, в отдельных точках она может быть равна нулю. Такие точки называются точками спрямления. Кривизна в каждой из точек плоской кривой а определяется с помощью соприкасающейся в этой точке окружности (рис.7.8). Соприкасающейся окружностью или кругом кривизны в данной точке называется предельное положение окружности, когда она проходит через данную точку и две другие бесконечно близкие к ней точки. Центр соприкасающейся окружности называется центром кривизны кривой в данной точке, а радиус такой окружности – радиусом кривизны кривой линии в данной точке. Множество центров кривизны кривой является кривая линия- её называют эволютой данной кривой, а кривая по отношению к своей эволюте называется эвольвентой.

Лекция №7-2

1. Проекцией кривой линии является кривая линия;

2. Касательная к кривой линии проецируется в касательную к её проекции;

3. Несобственная точка кривой проецируется в несобственную точку её проекции;

4. Порядок линии – проекции алгебраической кривой равен порядку самой кривой или меньше;

5. Число узловых точек ( в которых кривая пересекает сама себя) проекции равно числу узловых точек самой кривой.

Случаи когда, плоская кривая проецируется в прямую (свойства 1,4,5), а касательная в точку (свойство 2) не учитываются.

Пространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траекторию движения точки.

Пространственную, так же как и плоскую, кривую линию на чертеже задают последовательным рядом точек.

Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии.