Ordm;. Скорость точки в криволинейной системе координат. Лемма Лагранжа

Вывод второй формулы для расчета ковариантных координат скорости

Целью данного раздела является вывод следующей формулы (1.5.37) для ковариантных координат 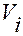скорости :

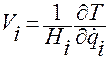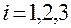, . (1.5.37)

где

.

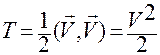Для ее вывода воспользуемся определением ковариантных координат и леммой Лагранжа.

Поскольку, согласно указанному определению

, , ,

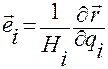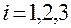то можем записать

.

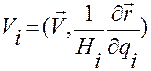
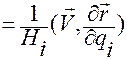Подставим соотношение а) из леммы Лагранжа в правую часть выражения построенного для :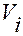

а) , .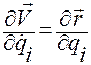

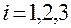Учтем, что задается формулой (1.5.32)

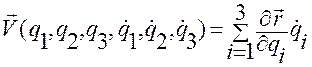, (1.5.32)

а для нее справедливо очевидное равенство

,

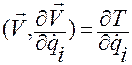в котором

.

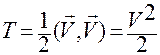В результате окончательно находим

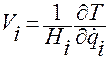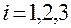, . (1.5.37)

Отметим здесь, что полученная формула (1.5.37) для 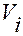отличается по виду от (1.5.31)

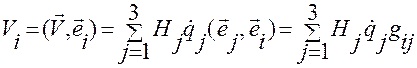, (1.5.31)

– от первой формулы, построенной для 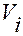в п.п. 8.2.3.

Однако очевидно, что она совпадает с (1.5.31), если учесть в (1.5.37), что функция 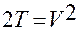задается правой частью равенства (1.5.30):

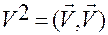
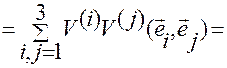
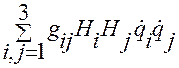. (1.5.30)

На практике часто бывает удобнее сначала построить функцию 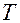, а затем для вычисления 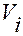применить формулу (1.5.37) вместо непосредственного применения (1.5.31).

8.7. Связь декартовых координат скорости
с обобщенными скоростями точки

Легко видеть, что

.

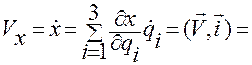
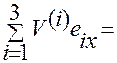
Отсюда круговой перестановкой координат 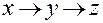и ортов 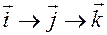получим выражения для 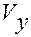и :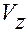

,

.

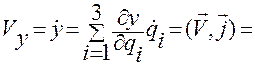
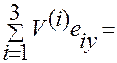
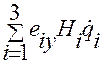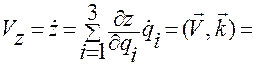
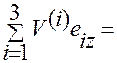
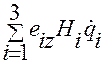В матричной записи эти выражения для 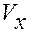, 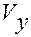и 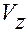примут вид:

,

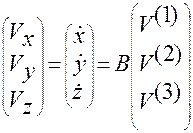где 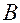— матрица перехода от аффинной системы к декартовой прямоугольной системе координат,

.

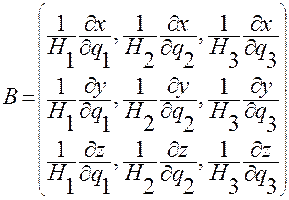В данном выражении элементы матрицы 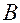вычисляются в точке 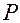(а не в точке ).

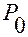1.3. Дополнение 3 к §5