Ускорение в декартовых координатах

Вычислим ускорение точки 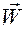согласно определению

.

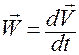Учтем, что

.

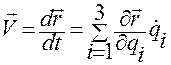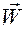Дифференцируя правую часть по , приходим к векторному представлению ускорения в зависимости от вектор-функции 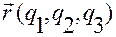, обобщенных скоростей 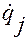и обобщенных ускорений , :

.

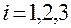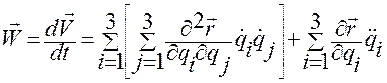В проекциях на абсолютные оси 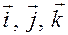оно примет вид:

,

,

.

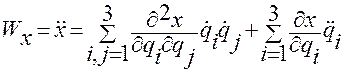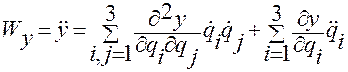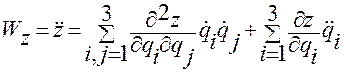9.2. Связь контравариантных координат ускорения с
его декартовыми координатами

Запишем теперь разложение ускорения 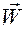по базису 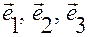основной системы с началом в точке 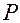и по базису 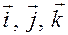ДПСК:

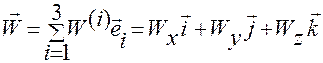. (1.5.38)

Умножая обе части равенства последовательно на 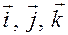скалярно, находим:

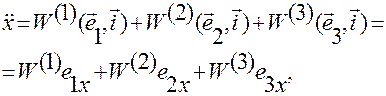
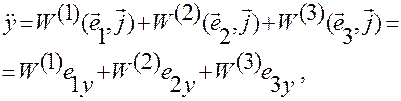
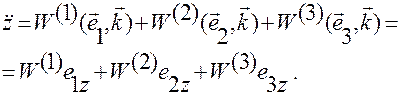
В матричном представлении данные соотношения примут вид:

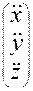
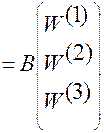, или .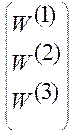

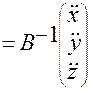Они дают связь контравариантных координат 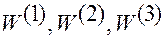ускорения 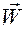с его декартовыми координатами .

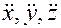Из равенства 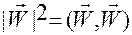подстановкой в него разложения (1.5.38)

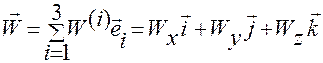. (1.5.38)

получаем формулу для :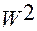

,

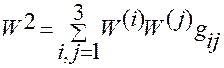где 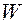— модуль ускорения .

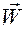2. Дополнения к главе 1 «Кинематика точки»