Определение 9

Система координат, для которой является матрицей перехода от фиксированной основной системы, называется согласованной с основной системой через матрицу .

Из (1.5.23)

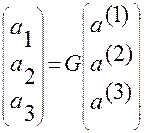(1.5.23)

следует, что союзная система является согласованной с основной через матрицу 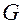метрических коэффициентов основной системы.

Поэтому координаты векторов 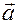в этой (союзной) системе называются ковариантными (слово «ковариантные» в переводе с французского означает «согласованно изменяющиеся»).

Они согласованно изменяются через матрицу .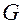

Основные координаты вектора 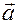могут быть вычислены через согласованные координаты 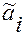(координаты этого вектора в новой системе координат) при фиксированной матрице по формуле

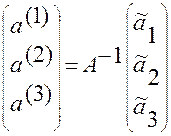. (1.5.25)

Очевидно, матрица 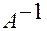является матрицей перехода от «новой» системы координат к «старой» (основной) системе.

В этом случае выражение (1.5.25) можем трактовать как обратный закон пересчета координат, а координаты 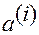вектора 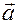в основной («старой») системе могут рассматриваться как координаты «противоположно меняющиеся» при фиксированной матрице по отношению к новым координатам.

Поэтому координаты вектора 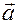в основной системе (координаты 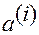) по отношению к союзной системе принято называть контравариантными координатами (при переводе с французского языка слово «контравариантные» означает «обратно изменяющиеся»).

Термин «контравариантные координаты» имеет и другой смысл.

А именно, он означает, что эти координаты меняются (рассчитываются) по обратному закону относительно некоторой фиксированной системы координат.

Если матрица задана, то согласно определению 9 эти координаты согласованы с заданной фиксированной системой координат через обратную матрицу .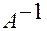

Применим это правило к основной и союзной системам координат.

Если считать, что координаты союзной системы фиксированы (заданы), а основной — пересчитываются по ним, то этот пересчет осуществляется с помощью обратной матрицы .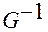

А тогда согласно указанному выше правилу:

координаты основной системы следует называть «контравариантными», поскольку они согласованы с фиксированными (союзными) через обратную матрицу .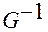

1.2. Дополнение 2 к §5