Ordm;. Ускорение точки в криволинейных координатах. Теорема Лагранжа

В конце этой лекции в Дополнении 1.3 к §5 в п.п. 9.1 выводятся формулы для вычисления ускорения точки в декартовых координатахпо ее криволинейным координатам, обобщенным скоростям и ускорениям. В п.п. 9.2 указанного Дополнения 1.3 описывается связь контравариантных координат ускорения с его декартовыми координатами.

Ниже, в п.п. 9.3 выведем формулу Лагранжадля вычисления ковариантных координат ускорения .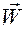

Ковариантные координаты ускорения точки

Построим формулу Лагранжадля вычисления ковариантных координат 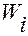, , 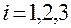ускорения .

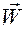Согласно определению ковариантных координат можем записать

, .

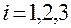Подставим в правую часть этого равенства значение орта 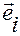, вычисленное в точке ,

.

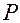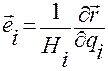Вынесем 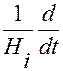за знак скалярного произведения.

В результате придем к следующему выражению для :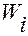

.

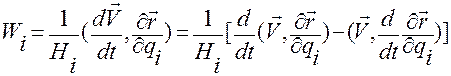В нем, в соответствии с определением понятия ускорения точки, производная 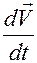вычисляется вдоль движения

, , .

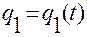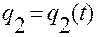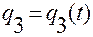Поэтому в множителе 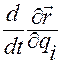производная по времени строится от суперпозиции функций 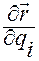и .

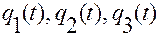А потому, согласно свойству б) функции 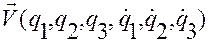из леммы Лагранжа, множитель 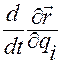можно заменить производной .

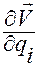Кроме того, по свойству а) из той же леммы, множитель 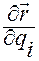можно заменить производной .

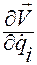А тогда выражение для 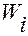примет вид

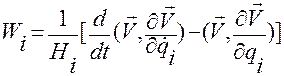. (1.5.39)

Введем функцию

,

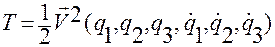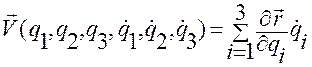
где задается формулой (1.5.32):

. (1.5.32)

Будем иметь

, .

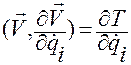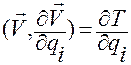Подставляя в (1.5.39)

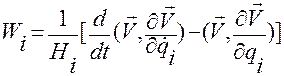, (1.5.39)

окончательно найдем

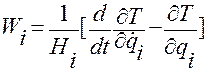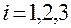, . (1.5.40)

Эта формуланазывается формулой Лагранжа для вычисления ковариантных координат ускорения точки.

Таким образом, доказали следующую теорему.