Абсолютное, относительное и переносное движения точки

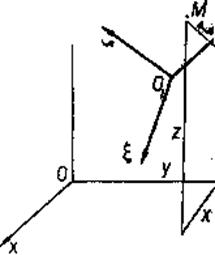
В ряде случаев приходится рассматривать движение точки по отношению к системе координат О₁ξηζ, которая, в свою очередь, движется по отношению к другой системе координат Охуz условно принятой в качестве неподвижной. В механике каждую из указан­ных систем координат связывают с некоторым телом. Например, рас­смотрим качение без скольжения колеса вагона по рель­су. С рельсом свяжем неподвижную систему координат Аху, а подвижную систему Oξη свяжем с центром колеса и предположим, что она движется поступательно. Движе­ние точки на ободе колеса является составным или сложным.

Введем следующие определения:

Движение точки относительно системы координат Охуz (рис. 53) называется абсолютным.

2. Движение точки относительно подвижной системы координат O₁ξηζ называется населенным.

3. Переносным движением точки называют движение той точки тела, связанного с подвижной системой координат О₁ ξηζ, относи­тельно неподвижной системы координат, с которой в данный момент совпадает рассматриваемая движущаяся точка.

Таким образом, переносное движение вызвано движением под­вижной системы координат по отношению к неподвижной. В приве­денном примере с колесом переносное движение точки обода колеса обусловлено поступательным движением системы координат О₁ ξηζ по отношению к неподвижной системе координат Аху.

Уравнения абсолютного движения точки получим, выразив коор­динаты точки х, у,z как функции времени:

х=х(t), у = у(t), z = z(t).