Ускорения точек тела, вращающегося вокруг неподвижной оси

Так как в рассматриваемом случае движение точки задано естест­венным способом, то полное ускорение точки можно вычислить, как векторную сумму касательного ω_τ и нормального ω_n ускорений (см. глава I, § 16). Выразим эти ускорения через кинематические характеристики вращательного движения тела, т. е_; через ω и ε.

Имеем ω_n= 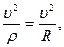ω_τ=s,

Откуда, на основании формул (11.66) и (11.67),

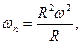
Или

ω_n = R ω²

и

ω_τ = s== Rφ,

Или

ω_τ = Rε.

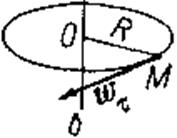
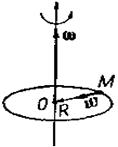
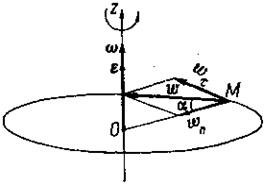
Следовательно, нормальное ускорение точки тела при вращении его вокруг неподвижной оси равно произведению радиуса вращения на квадрат угловой скорости. Касательное ускорение равно произведе­нию радиуса вращения на угловое ускорение. Нормальное ускорение направлено по радиусу вращения к центру вращения (рис. 51, а). Касательное ускорение направлено по касательной к траектории в сторону вращения, если движение ускоренное (ε > 0), и в сторо­ну, противоположную вращению, если движение замедленное, т. е. ε< 0 (рис. 51, б, в).