Анализ ускорения Кориолиса.

Рассмотрим линейное движение точки вдоль радиуса вращающегося колеса. Пусть за время дельта Т точка М переместилась в положение М1, тогда линейная переносная скорость В(е) 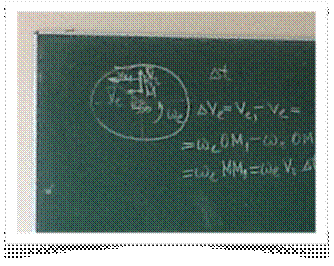изменится на величину. Тогда ускорение равно пределу отношения прикрашения функции к приращению аргумента. Таким образом скорость переносного движения изменяется по величине из-за наличия относительного движения. Рассмотрим изменение относительной скорости по направлению за время дельта Т.

Оно имеет такую же величину, отсюда и удвоенный коэффициент. Скорость изменяется по направлению из-за наличия переносного и вращательного движения. Оба эти эффекта взаимного влияния переносного и относительного движений выражаются в ускорении Кориолиса.