Вектор ускорения в данный момент времени определяется как первая производная от вектора скорости по времени или вторая производная от радиуса-вектора по времени.
 Поскольку скорость величина векторная, она может изменяться как по величине, так и по направлению. Изменение вектора скорости
Поскольку скорость величина векторная, она может изменяться как по величине, так и по направлению. Изменение вектора скорости 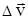 можно представить в виде суммы двух слагаемых векторов
можно представить в виде суммы двух слагаемых векторов 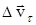 и
и 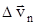 т.е.
т.е. 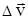 =
= 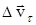 +
+ 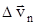 , где
, где 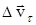 - изменение скорости по величине,
- изменение скорости по величине, 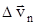 - изменение скорости по направлению за промежуток времени Dt. Поэтому вводят две составляющие ускорения:
- изменение скорости по направлению за промежуток времени Dt. Поэтому вводят две составляющие ускорения: 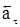 - тангенциальное или касательное ускорение,
- тангенциальное или касательное ускорение, 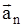 - нормальное ускорение. Полное ускорение
- нормальное ускорение. Полное ускорение 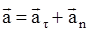 , где
, где 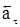 - характеризует изменение скорости только по величине, а
- характеризует изменение скорости только по величине, а 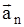 - характеризует изменение скорости только по направлению. На основании вышеизложенного можно записать мгновенное ускорение
- характеризует изменение скорости только по направлению. На основании вышеизложенного можно записать мгновенное ускорение
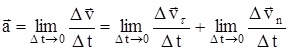 ,
,
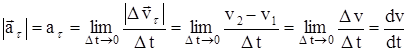
Тангенциальное ускорение  численно равно первой производной от скорости по времени и направлено по касательной к траектории в данной точке. Вот почему
численно равно первой производной от скорости по времени и направлено по касательной к траектории в данной точке. Вот почему 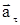 называется еще касательным ускорением.
называется еще касательным ускорением.
Учитывая, что 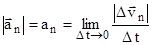 , можно геометрическими построениями и расчетами получить
, можно геометрическими построениями и расчетами получить 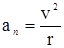 . Вектор
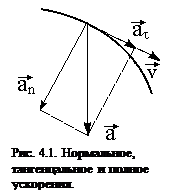
. Вектор 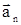 перпендикулярен траектории в данной точке (направлен по радиусу кривизны траектории к центру), отсюда его название – центростремительное ускорение. Полное ускорение численно равно
перпендикулярен траектории в данной точке (направлен по радиусу кривизны траектории к центру), отсюда его название – центростремительное ускорение. Полное ускорение численно равно
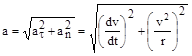 .
.
Вектор 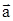 является диагональю прямоугольника со сторонами
является диагональю прямоугольника со сторонами 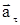 и
и 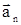 (рис.4.1).
(рис.4.1).
1. 3. Частные случаи движения.@
1. Равномерное прямолинейное движение: 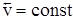 ;
; 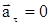 ;
; 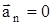 ;
; 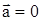 .
.
Уравнение движения: 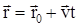 или
или 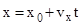 ;
; 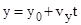 ;
; 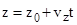 .
.
2. Прямолинейное равнопеременное движение: 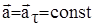 ,
, 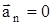 ;
; 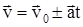
При равноускоренном движении а>0, при равнозамедленном а<0. Уравнение движения: 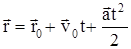 или
или
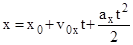 ,
, 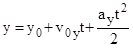 ,
, 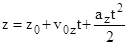 .
.
Уравнение пути, пройденного точкой при равнопеременном движении, можно получить при интегрировании формулы 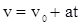 по времени от 0 до t.
по времени от 0 до t.
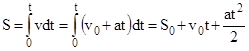
3. Прямолинейное переменное движение: 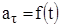 ,
, 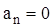
4. Равномерное криволинейное движение: 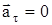 ,
, 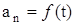
5. Равномерное движение по окружности: 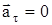 ,
, 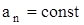 ,
, 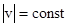 ,
, 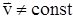 . Этот вид движения следует рассмотреть подробнее.
. Этот вид движения следует рассмотреть подробнее.
1. 4. Кинематические характеристики вращательного движения. @
Дата добавления: 2015-08-01; просмотров: 2204;
