Вращательным называется такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
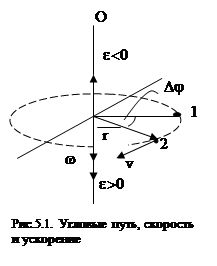 Пусть точка или абсолютно твердое тело за время Dt, вращаясь вокруг неподвижной оси ОО’, перешло из положения 1 в 2, повернувшись на угол Dj. Скалярная величина Dj есть угловой путь (рис.5.1). Элементарные (бесконечно малые) повороты можно рассматривать как векторы. Модуль такого вектора равен углу поворота dj, а направление определяется по правилу правого винта: если винт вращать в направлении движения точки по окружности, то поступательное движение его острия указывает направление вектора
Пусть точка или абсолютно твердое тело за время Dt, вращаясь вокруг неподвижной оси ОО’, перешло из положения 1 в 2, повернувшись на угол Dj. Скалярная величина Dj есть угловой путь (рис.5.1). Элементарные (бесконечно малые) повороты можно рассматривать как векторы. Модуль такого вектора равен углу поворота dj, а направление определяется по правилу правого винта: если винт вращать в направлении движения точки по окружности, то поступательное движение его острия указывает направление вектора 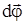 . Такие вектора, направление которых связывается с направлением вращения, называются псевдовекторами. Быстрота вращения характеризуется вектором угловой скорости
. Такие вектора, направление которых связывается с направлением вращения, называются псевдовекторами. Быстрота вращения характеризуется вектором угловой скорости 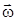 , направленной вдоль оси вращения как и
, направленной вдоль оси вращения как и 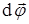 . Средняя угловая скорость
. Средняя угловая скорость 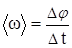 . Мгновенная угловая скорость
. Мгновенная угловая скорость 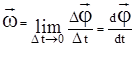 . Изменение
. Изменение 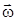 со временем определяет вектор углового ускорения
со временем определяет вектор углового ускорения 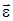 . Среднее угловое ускорение
. Среднее угловое ускорение 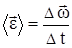 . Мгновенное угловое ускорение
. Мгновенное угловое ускорение 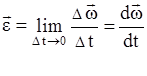 ;
;  . При вращении тела вокруг неподвижной оси изменение вектора
. При вращении тела вокруг неподвижной оси изменение вектора 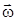 обусловлено только изменением его численного значения. Поэтому
обусловлено только изменением его численного значения. Поэтому 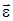 направлен вдоль оси вращения. Если вращение ускоренное, то направления
направлен вдоль оси вращения. Если вращение ускоренное, то направления 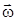 и
и 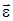 совпадают (e>0); если замедленное – то они противоположны (e<0). При равнопеременном движении точки по окружности (e=const)
совпадают (e>0); если замедленное – то они противоположны (e<0). При равнопеременном движении точки по окружности (e=const) 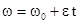 ,
, 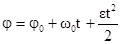 , где j0 – начальный угол поворота, w0 – начальная угловая скорость.
, где j0 – начальный угол поворота, w0 – начальная угловая скорость.
1. 5. Связь между линейными и угловыми кинематическими характеристиками. @
Пусть за малый промежуток времени dt материальная точка повернулась относительно оси вращения на малый угол dj (рис.6.1). По ранее приведенной формуле линейная скорость 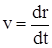 . При малых углах поворота перемещение dr можно считать равным произведению радиуса вращения r на угол поворота dj, т.е.
. При малых углах поворота перемещение dr можно считать равным произведению радиуса вращения r на угол поворота dj, т.е. 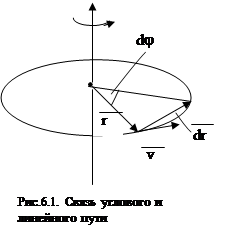
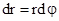 . Отсюда
. Отсюда  =rw. В векторном виде связь линейной скорости
=rw. В векторном виде связь линейной скорости 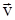 и угловой
и угловой 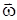 можно представить с помощью векторного произведения
можно представить с помощью векторного произведения 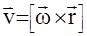 ,
,  . При вращении вокруг неподвижной оси угол между векторами
. При вращении вокруг неподвижной оси угол между векторами 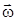 и
и 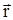 равен
равен 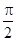 , следовательно
, следовательно 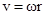 . Отсюда можно получить еще одно выражение для тангенцального ускорения
. Отсюда можно получить еще одно выражение для тангенцального ускорения 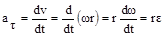 . Учитывая направление, связь тангенциального и углового ускорений можно записать в векторном виде
. Учитывая направление, связь тангенциального и углового ускорений можно записать в векторном виде 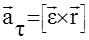 , а также для
, а также для 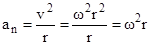 или
или  . Знак «минус» в формуле обусловлен противоположной направленностью векторов
. Знак «минус» в формуле обусловлен противоположной направленностью векторов 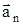 и
и 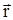 .
.
Если вращение равномерное, то 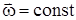 , и его можно характеризовать периодом вращения Т. Т – время одного полного оборота точки (тела) вокруг оси.
, и его можно характеризовать периодом вращения Т. Т – время одного полного оборота точки (тела) вокруг оси.
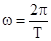 ;
; 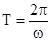 ;
; 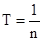 ;
; 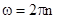
n – число оборотов в единицу времени, частота вращения. При равномерном вращении 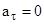 ,
, 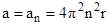 .
.
2. ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ. @
Динамика – это раздел механики, который изучает движение совместно с причинами, вызывающими или изменяющими это движение. В основе динамики лежат три закона Ньютона, сформулированные им в 1687 г.
Масса тела, силовое поле, сила. @
Масса тела (материальной точки) – скалярная физическая величина, одна из основных характеристик материи. Она определяет ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. Доказано, что инертная и гравитационная масса равны.
Поле физическое или силовое поле – есть форма существования материи, посредством которой осуществляются взаимодействия между макроскопическими телами или частицами, входящими в состав вещества. К физическим полям относятся гравитационное, электромагнитное, поле ядерных сил. Источниками полей служат незаряженные и заряженные тела, постоянные магниты, контуры с током, ядра атомов и т.д.
Причиной изменения движения тел является силовое воздействие.Сила 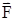 - векторная физическая величина, являющаяся мерой воздействия на тело со стороны других тел или полей, в результате чего тело либо приобретает ускорение, либо деформируется. Взаимодействие тел возможно как при соприкосновении, так и на расстоянии, благодаря силовым полям. В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Силы, связанные с перечисленными выше физическими полями, являются первичными, их называют фундаментальными силами. Имеется также множество вторичных сил, которые являются комбинацией фундаментальных сил (в основном – электромагнитные). Например, это силы межатомного и межмолекулярного взаимодействия, силы трения, силы деформации и др.
- векторная физическая величина, являющаяся мерой воздействия на тело со стороны других тел или полей, в результате чего тело либо приобретает ускорение, либо деформируется. Взаимодействие тел возможно как при соприкосновении, так и на расстоянии, благодаря силовым полям. В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Силы, связанные с перечисленными выше физическими полями, являются первичными, их называют фундаментальными силами. Имеется также множество вторичных сил, которые являются комбинацией фундаментальных сил (в основном – электромагнитные). Например, это силы межатомного и межмолекулярного взаимодействия, силы трения, силы деформации и др.
Гравитационное поле – это поле сил взаимодействия (притяжения) тел, имеющих массу. И. Ньютон установил, что для материальных точек формула величины силы гравитации имеет вид  , где G- гравитационная постоянная, m1 и m2 – массы взаимодействующих точек, r- расстояние между ними.
, где G- гравитационная постоянная, m1 и m2 – массы взаимодействующих точек, r- расстояние между ними.
Электромагнитное поле – это поле сил взаимодействия (притяжения или отталкивания) тел, имеющих электрический заряд. Формулы этих сил будут рассмотрены при изучении электрических и магнитных явлений.
Ядерное поле – это поле сил взаимодействия элементарных частиц, из которых состоят атомы и молекулы. Эти силы действуют только на очень малых расстояниях, их свойства рассматриваются при изучении ядер атомов.
2.2. Законы И.Ньютона. @
Классическая динамика базируется на трех законах Ньютона.
Первый закон Ньютона: Если на материальную точку не действуют силы или приложенные силы взаимноуравновешены (т.е. суммарная или результирующая сила равна нулю), то материальная точка будет находиться в состоянии покоя ( 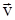 =0) или равномерного прямолинейного движения (
=0) или равномерного прямолинейного движения ( 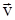 =const).
=const).
Понятия движения и покоя относительны и зависят от выбора системы отсчета. Свойство тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Первый закон Ньютона называют законом инерции. Система отсчета, в которой он выполняется, считается инерциальной. Экспериментально установлено, что гелиоцентрическую систему отсчета можно считать инерциальной, а геоцентрическая, строго говоря, неинерциальна. Однако, для решения многих простых задач и ее считают инерциальной.
Второй закон Ньютона.Скорость изменения импульса движущейся материальной точки (тела) равна действующей на нее силе:
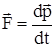 .
.
Векторная физическая величина равная произведению массы точки на вектор скорости называется импульсом (количеством движения) точки 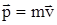 .Последнюю формулу можно записать в виде
.Последнюю формулу можно записать в виде 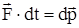 , где
, где 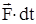 - элементарный импульс силы, действующий на точку (тело),
- элементарный импульс силы, действующий на точку (тело), 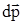 - изменение импульса точки (тела). Если на точку (тело) действует постоянная сила
- изменение импульса точки (тела). Если на точку (тело) действует постоянная сила 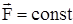 , то из предыдущей формулы имеем
, то из предыдущей формулы имеем 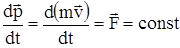 . Умножим обе части равенства на dt
. Умножим обе части равенства на dt 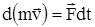 и интегрируя обе части равенства, получим
и интегрируя обе части равенства, получим
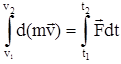 ,
, 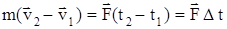 .
.
Изменение импульса тела под действием постоянной силы равно произведению этой силы на время ее действия или импульсу силы.
Кроме общей формулировки II закона Ньютона часто используют формулировку для случая, когда масса не меняется со временем. Учитывая, что 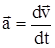 , второй закон Ньютона можно записать в виде:
, второй закон Ньютона можно записать в виде: 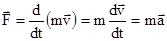 или
или 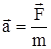 .
.
Дата добавления: 2015-08-01; просмотров: 2183;
