Соединяющей эти точки
.
Эти силы приложены к разным материальным точкам (телам), всегдадействуют парами и являются силами одной природы. Закон справедлив для описания взаимодействия покоящихся тел, а также в случае контактных взаимодействий.
Пример: Пусть тело массой m лежит на горизонтальной поверхности.
Тело действует на нее с силой 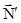 , направленной вертикально вниз. Поверхность же действует на тело с силой
, направленной вертикально вниз. Поверхность же действует на тело с силой 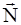 (реакция опоры), равной по модулю силе
(реакция опоры), равной по модулю силе 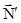 . На тело также действует сила тяжести
. На тело также действует сила тяжести 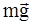 . Так как тело находится в покое то, очевидно,
. Так как тело находится в покое то, очевидно, 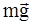 = -
= - 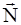 и все эти силы равны по модулю (рис.2.2.).
и все эти силы равны по модулю (рис.2.2.).
2. 3. Закон сохранения импульса. @
Рассмотрим общий случай - систему n взаимодействующих материальных точек (тел). На каждое тело действуют внутренние и внешние силы. Силы взаимодействия между телами системы называются внутренними, а силы, которые действуют со стороны тел, не входящих в рассматриваемую систему, называются внешними. Массы точек - m1, m2, ..., mn, скорости их движения - v1, v2,...,vn. Пусть 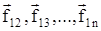 - внутренние силы, действующие на первую точку со стороны второй, третьей и т.д.
- внутренние силы, действующие на первую точку со стороны второй, третьей и т.д. 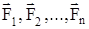 - внешние силы, действующие на первую, вторую и т.д. материальные точки (рис.2.3.).
- внешние силы, действующие на первую, вторую и т.д. материальные точки (рис.2.3.).
Так как внутренние силы являются силами взаимодействия между телами, то они должны подчиняться третьему закону Ньютона 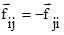 .
.
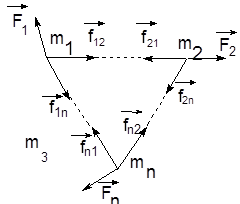 Рис.2.3. Силы взаимодействия в системе n материальных точек.
Рис.2.3. Силы взаимодействия в системе n материальных точек.
|
Запишем II закон Ньютона для каждого из n тел:
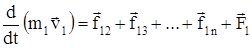
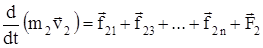
. . . . . .
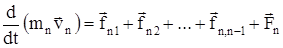 .
.
Если просуммировать эти уравнения по всем телам и учесть, что при двойном суммировании внутренних сил, согласно третьему закону Ньютона
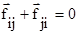 , то получаем
, то получаем 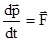 , где
, где 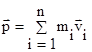 ,
, 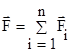 .
.
Если система замкнутая, т.е. на нее не действуют внешние силы, то 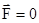 ,
, 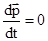 , т.е.
, т.е. 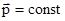 .
.
Дата добавления: 2015-08-01; просмотров: 839;
