Где: А – совершаемая работа, Е1 и Е2 - энергии системы в начальном и конечном состояниях.
 Сила, приложенная к телу, совершает работу, если тело перемещается.Если тело движется прямолинейно и на него действует постоянная сила, направленная под углом a к перемещению, то работа равна скалярному произведению векторов перемещения и силы (рис.2.6)
Сила, приложенная к телу, совершает работу, если тело перемещается.Если тело движется прямолинейно и на него действует постоянная сила, направленная под углом a к перемещению, то работа равна скалярному произведению векторов перемещения и силы (рис.2.6)  ,где
,где 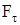 - касательная составляющая силы, т.е. проекция
- касательная составляющая силы, т.е. проекция 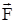 на
на 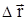 .Если же сила переменна по величине и по направлению или перемещение не прямолинейно, то траекторию движения разбивают на малые участки dS - так, чтобы участок можно было бы считать прямолинейным и силу, действующей на нем - постоянной (рис.2.7). Тогда работа на этом участке
.Если же сила переменна по величине и по направлению или перемещение не прямолинейно, то траекторию движения разбивают на малые участки dS - так, чтобы участок можно было бы считать прямолинейным и силу, действующей на нем - постоянной (рис.2.7). Тогда работа на этом участке  , а работа на всем пути равна сумме всех элементарных работ
, а работа на всем пути равна сумме всех элементарных работ 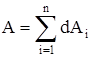 . При
. При 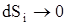
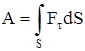 . Для вычисления такого интеграла надо знать зависимость
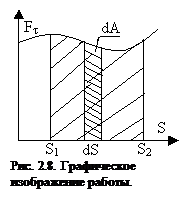
. Для вычисления такого интеграла надо знать зависимость 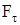 от S. Если эту зависимость представить графически (рис.2.8), тогда работа силы по перемещению из S1 в S2 численно равна площади заштрихованной фигуры, ограниченной кривой F(S), координатной осью S и двумя вертикальными прямыми S1 и S2. Сила не совершает работу (А=0), если Dr=0 или
от S. Если эту зависимость представить графически (рис.2.8), тогда работа силы по перемещению из S1 в S2 численно равна площади заштрихованной фигуры, ограниченной кривой F(S), координатной осью S и двумя вертикальными прямыми S1 и S2. Сила не совершает работу (А=0), если Dr=0 или 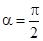 . Если a<
. Если a< 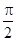 , то А>0; если a>
, то А>0; если a> 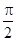 , то А<0. При одновременном действии на тело нескольких сил, работа равна алгебраической сумме работ составляющих сил
, то А<0. При одновременном действии на тело нескольких сил, работа равна алгебраической сумме работ составляющих сил 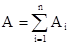 .
.
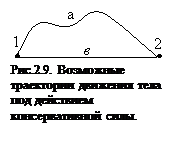
 Сила F называется консервативной, если совершаемая ею работа не зависит от формы траектории, а зависит от начального и конечного положений точки (тела). На рис.2.9. изображены две различные траектории движения тела под действием некоторой консервативной силы. Работа, совершаемая данной силой на пути 1а2 равна А1а2. Работа, совершаемая на пути 2а1, будет отрицательной и А1а2 = - А2а1. Поскольку совершаемая работа не зависит от формы траектории, мы можем записать:
Сила F называется консервативной, если совершаемая ею работа не зависит от формы траектории, а зависит от начального и конечного положений точки (тела). На рис.2.9. изображены две различные траектории движения тела под действием некоторой консервативной силы. Работа, совершаемая данной силой на пути 1а2 равна А1а2. Работа, совершаемая на пути 2а1, будет отрицательной и А1а2 = - А2а1. Поскольку совершаемая работа не зависит от формы траектории, мы можем записать:  ,
,  или
или 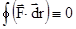 , где
, где  - означает интегрирование вдоль замкнутой траектории или интеграл по контуру. Отсюда следует важное свойство консервативных сил - при перемещении материальной точки (тела) вдоль замкнутой траектории работа консервативной силы тождественно равна нулю. Сила всемирного тяготения, сила упругости – консервативные силы. Силы, неудовлетворяющие этому условию называют неконсервативными или диссипативными. Примером таких сил служат силы трения.
- означает интегрирование вдоль замкнутой траектории или интеграл по контуру. Отсюда следует важное свойство консервативных сил - при перемещении материальной точки (тела) вдоль замкнутой траектории работа консервативной силы тождественно равна нулю. Сила всемирного тяготения, сила упругости – консервативные силы. Силы, неудовлетворяющие этому условию называют неконсервативными или диссипативными. Примером таких сил служат силы трения.
 Для характеристики скорости совершения работы вводится понятие мощности. Мощностью, развиваемой силой
Для характеристики скорости совершения работы вводится понятие мощности. Мощностью, развиваемой силой 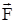 , называется скалярная физическая величина, численно равная работе, совершаемой этой силой за единицу времени
, называется скалярная физическая величина, численно равная работе, совершаемой этой силой за единицу времени 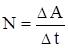 .Если в разные моменты времени dt совершаются разные работы, то используют понятие мгновенной мощности
.Если в разные моменты времени dt совершаются разные работы, то используют понятие мгновенной мощности 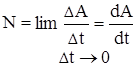 .
.
Для движущихся тел можно получить формулу мгновенной мощности
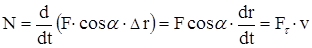 или
или 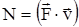 ,
,
т.е. мощность равна скалярному произведению векторов силы и скорости.
Важное требование, предъявляемое к любому двигателю - это способность совершать большую работу за единицу времени, т.е. иметь большую мощность. Из полученной формулы следует, что для достижения этой цели необходимо либо увеличить силу тяги, развиваемую двигателем (например, автомобиля), либо увеличить его быстроходность. Первый путь связан с увеличением силовых нагрузок на все движущиеся части двигателя (поршни, коленчатый вал и т.д.), а они имеют ограниченную прочность. Чтобы детали смогли выдерживать действие больших нагрузок, нужно увеличивать их размеры, делать их более массивными. Поэтому все мощные тихоходные машины необычайно громоздкие. Второй путь позволяет получить большие мощности при малых силовых нагрузках на детали двигателя и меньших его размерах. В современное время этот путь наиболее перспективен.
2.7. Кинетическая и потенциальная энергии. @
Полная механическая энергия Ем складывается из кинетической Ек и потенциальной Еп энергий Ем = Ек + Еп .
Кинетическая энергия Ек – это энергия движущегося тела, она равна работе, которую могло бы совершать тело при торможении до полной остановки Ек=Атор. Соответственно, эта работа численно равна работе внешней силы по увеличению скорости тела от 0 до 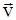 т.е. Ек=Аразгона.Рассчитаем эту работу, учитывая, что работа внешней силы F над телом на малом участке перемещения dr равна (здесь использован второй закон Ньютона, соотношение
т.е. Ек=Аразгона.Рассчитаем эту работу, учитывая, что работа внешней силы F над телом на малом участке перемещения dr равна (здесь использован второй закон Ньютона, соотношение 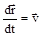 и законы дифференцирования)
и законы дифференцирования)
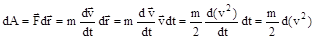 .
.
Так как по определению  , то получаем
, то получаем 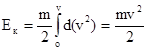 .
.
 Если система состоит из n движущихся точек (тел), то ее полная кинетическая энергия равна
Если система состоит из n движущихся точек (тел), то ее полная кинетическая энергия равна
 . Если система обладает только кинетической энергией, то изменение кинетической энергии тела равно работе сил, действовавших на тело во время движения
. Если система обладает только кинетической энергией, то изменение кинетической энергии тела равно работе сил, действовавших на тело во время движения 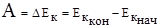 .
.
Потенциальная энергия Еп – это энергия взаимодействия тел системы, определяемая взаимным расположением тел и характером сил взаимодействия между ними. Потенциальная энергия - величина, зависящая от выбора начального положения, при котором Еп=0, т.е. она величина относительная. Если работу совершают консервативные силы, то происходит изменение Еп системы на величину  . Конкретный вид зависимости Еп от расположения тел системы связан с характером сил взаимодействия тел.
. Конкретный вид зависимости Еп от расположения тел системы связан с характером сил взаимодействия тел.
Рассмотрим два примера:
 1). Определим Еп тела, поднятого над землей т.е. энергию взаимодействия этого тела с планетой Земля. Известно, что на тело действует консервативная сила тяжести, при небольших высотах h она мало меняется и считается по формуле P = mg. При падении тела сила тяжести совершает работу A=mgh, при этом потенциальная энергия тела уменьшается ровно на эту величину. Если Еп1- потенциальная энергия тела, поднятого над землей, а Еп2 - потенциальная энергия тела на поверхности земли, которую принято считать равной нулю, то из связи работы и изменения энергии, получим
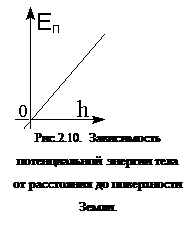
1). Определим Еп тела, поднятого над землей т.е. энергию взаимодействия этого тела с планетой Земля. Известно, что на тело действует консервативная сила тяжести, при небольших высотах h она мало меняется и считается по формуле P = mg. При падении тела сила тяжести совершает работу A=mgh, при этом потенциальная энергия тела уменьшается ровно на эту величину. Если Еп1- потенциальная энергия тела, поднятого над землей, а Еп2 - потенциальная энергия тела на поверхности земли, которую принято считать равной нулю, то из связи работы и изменения энергии, получим 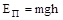 . График зависимости Еп от h представлен на рис.2.10. Ясно, что Еп1>0 при h>0, т.е. над землей и Еп2<0 при h<0, т.е. ниже уровня земли.
. График зависимости Еп от h представлен на рис.2.10. Ясно, что Еп1>0 при h>0, т.е. над землей и Еп2<0 при h<0, т.е. ниже уровня земли.
2). Определим потенциальную энергию упруго деформированной пружины. Из экспериментов известно, что при сжатии (растяжении) пружины в ней возникает сила упругости  . Знак минус показывает, что сила упругости направлена в сторону противоположную деформации. Работа этой силы затрачивается на увеличение потенциальной энергии пружины т.е. A=DEп= Еп2- Еп1 . Так как dA=Fdx=kxdx, то
. Знак минус показывает, что сила упругости направлена в сторону противоположную деформации. Работа этой силы затрачивается на увеличение потенциальной энергии пружины т.е. A=DEп= Еп2- Еп1 . Так как dA=Fdx=kxdx, то 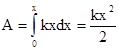 (Еп недеформированной пружины считается равной нулю). Следовательно
(Еп недеформированной пружины считается равной нулю). Следовательно 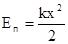 , на рис.2.11 представлен ее график.
, на рис.2.11 представлен ее график.
2.8. Связь потенциальной энергии тела и действующей на него консервативной силы. @
Так как работа консервативной силы равна убыли потенциальной энергии, то 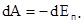 или
или 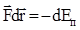 . Высшая математика позволяет выразить малое изменение любой функции (дифференциал функции) через частные производные от этой функции по ее аргументам. Конкретно для дифференциала потенциальной энергии, зависящей от координат, можно получить
. Высшая математика позволяет выразить малое изменение любой функции (дифференциал функции) через частные производные от этой функции по ее аргументам. Конкретно для дифференциала потенциальной энергии, зависящей от координат, можно получить 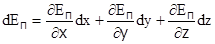 . Если подставить это выражение в
. Если подставить это выражение в 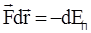 , то после записи левой части через проекции силы на оси координат, получим
, то после записи левой части через проекции силы на оси координат, получим
 .
.
Это выражение должно быть справедливо при любых малых перемещениях dx, dy, dz, что может быть только тогда, когда выполняются соотношения 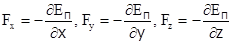 .
.
Дата добавления: 2015-08-01; просмотров: 1642;
