В результате получаем связь между Еп и F, в векторной форме ее записывают сокращенно в виде
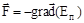 ,
,
где используют математический символ для вектора, который называется градиентом скалярной величины Еп и обозначается grad (Еп) 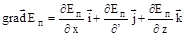 .
.
2.9. Закон сохранения и превращения энергии в механике. @
В 1748 г. М.В.Ломоносов сформулировал закон сохранения материи и движения. Через 100 лет Р.Майер и Г.Гельмгольц дали количественную формулировку закона сохранения и превращения энергии.
В замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела другому, но общее количество энергии остается неизменным. В природе и технике постоянно имеют место превращения одних видов энергии в другие. Например, в электродвигателях электрическая энергия переходит в механическую, в ядерном реакторе ядерная энергия переходит в тепловую, затем в механическую и электромагнитную, при фотоэффекте - электромагнитная в электрическую и т.д. Однако следует иметь в виду, что одновременно может происходить несколько типов превращений энергии, например, обычно некоторая часть энергии непременно превращается во внутреннюю (тепловую) энергию вещества (в энергию теплового движения молекул). Но всегда общий запас энергии системы в любой момент времени остается неизменным. Закон сохранения и взаимопревращения энергии является всеобщим законом природы, не имеющим исключений; если он как бы нарушается в эксперименте, значит что-то не учтено.
Закон сохранения механической энергии формулируется следующим образом: Если в замкнутой системе действуют консервативные силы, то механическая энергия не переходит в другие виды и остается постоянной во времени (при этом возможен переход потенциальной энергии в кинетическую и наоборот) 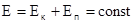 .
.
Продемонстрируем действие этого закона на примере свободного падения тела.
 Пример: Пусть тело массой m начинает падать вниз с высоты h.
Пример: Пусть тело массой m начинает падать вниз с высоты h.
Рассчитаем его механическую энергию в различные моменты времени. В начальный момент времени, в верхней точке его механическая энергия равна mgh (Ек =0 так как начальная скорость равна нулю).
Если не учитывать силы трения о воздух, то в любой следующий момент времени t координату и скорость тела можно рассчитать с помощью законов кинематики для равноускоренного движения с ускорением свободного падения g (см. рис.2.12): z = h ‑ gt2/2, v = ‑ gt.
Механическая энергия в этот момент времени будет равна
Ем = Еп + Ек = mgz + mv2/2 = mg(h – gt2/2) + m(gt)2/2 = mgh, т.е. равна энергии в начальный момент времени. Отсюда видно, что механическая энергия не меняется со временем. Если же рассматривать и действие сил трения, то окажется, что механическая энергия тела при движении уменьшается. Это объясняется частичным превращением ее во внутреннюю (тепловую) энергию воздуха и самого тела.
3. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. @
3.1. Основные характеристики динамики вращательного движения. @
Для описания вращательного движения используются следующие параметры : момент инерции J, момент силы 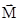 , момент импульса тела
, момент импульса тела 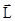 . Аналогами их в поступательном движении являются масса m, сила
. Аналогами их в поступательном движении являются масса m, сила 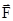 , импульс тела
, импульс тела 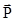 .
.
Момент инерции материальной точки относительно некоторой оси есть скалярная физическая величина равная произведению массы этой точки на квадрат кратчайшего расстояния от нее до оси вращения .
 Чтобы рассчитать момент инерции твердого тела, его мысленно разбивают на n материальных точек с массами Dm1, Dm2,..., Dmn, находящихся на расстояниях r1, r2,..., rn от оси вращения. Момент инерции твердого тела J, вращающегося вокруг неподвижной оси равен алгебраической сумме моментов инерции всех точек, из которых состоит тело
Чтобы рассчитать момент инерции твердого тела, его мысленно разбивают на n материальных точек с массами Dm1, Dm2,..., Dmn, находящихся на расстояниях r1, r2,..., rn от оси вращения. Момент инерции твердого тела J, вращающегося вокруг неподвижной оси равен алгебраической сумме моментов инерции всех точек, из которых состоит тело 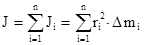 . При непрерывном распределении масс тела эта сумма сводится к интегралу
. При непрерывном распределении масс тела эта сумма сводится к интегралу 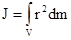 , где V - объем тела, r – кратчайшее расстояние от точки до оси вращения. На основании этой формулы рассчитываются моменты инерции тел различной формы. Например: 1) полый тонкостенный цилиндр или обруч радиуса R, массой m и осью вращения, совпадающей с осью симметрии
, где V - объем тела, r – кратчайшее расстояние от точки до оси вращения. На основании этой формулы рассчитываются моменты инерции тел различной формы. Например: 1) полый тонкостенный цилиндр или обруч радиуса R, массой m и осью вращения, совпадающей с осью симметрии 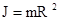 ; 2) сплошной цилиндр или диск радиуса R, массой m и осью вращения, совпадающей с осью симметрии
; 2) сплошной цилиндр или диск радиуса R, массой m и осью вращения, совпадающей с осью симметрии 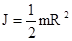 ; 3) шар радиуса R, массой m и осью вращения, проходящей через его центр
; 3) шар радиуса R, массой m и осью вращения, проходящей через его центр 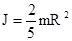 . Приведенные примеры показывают, что момент инерции тела зависит от его массы, формы, геометрических размеров, его расположения относительно оси вращения, распределения массы по объему тела.
. Приведенные примеры показывают, что момент инерции тела зависит от его массы, формы, геометрических размеров, его расположения относительно оси вращения, распределения массы по объему тела.
Расчет моментов инерции тел относительно осей, не совпадающих с осью симметрии более сложен. В таких случаях применяется теорема Штейнера: момент инерции любого тела относительно произвольной оси ОО¢ равен сумме момента инерции этого тела JO относительно оси АА¢ , параллельной данной и проходящей через центр масс тела С, и произведения массы тела на квадрат расстояния между осями (рис.3.1) 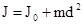 .
.
Моментом силы относительно неподвижной точки О называется векторная физическая величина, равная векторному произведению радиуса-вектора , проведенного из точки О в точку приложения силы, на вектор силы: .
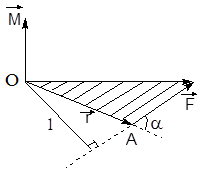 Рис.3.2. Момент силы относительно неподвижной точки.
Рис.3.2. Момент силы относительно неподвижной точки.
|
Направление  перпендикулярно плоскости, в которой лежат вектора
перпендикулярно плоскости, в которой лежат вектора  и
и 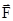 . Его направление совпадает с направлением поступательного движения правого винта при его вращении от
. Его направление совпадает с направлением поступательного движения правого винта при его вращении от 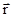 к
к 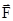 (рис.3.2). Модуль момента силы
(рис.3.2). Модуль момента силы
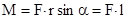 ,
, 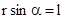 - плечо силы - кратчайшее расстояние между линией действия силы и точкой О. Если к точке А приложено несколько сил, то результирующий
- плечо силы - кратчайшее расстояние между линией действия силы и точкой О. Если к точке А приложено несколько сил, то результирующий 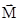 будет равен векторной сумме моментов слагаемых сил:
будет равен векторной сумме моментов слагаемых сил:
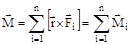
Момент силы, действующей на тело относительно неподвижной оси z, есть скалярная величина Mz, равная проекции на эту ось вектора момента силы, определенного относительно произвольной точки О данной оси z (рис.3.3) 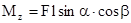 .
.
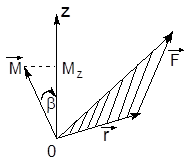 Рис.3.3. Момент силы относительно неподвижной оси.
Рис.3.3. Момент силы относительно неподвижной оси.
|
Значение момента Mz не зависит от положения точки О на оси z. Если ось z совпадает с направлением вектора 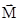 , то момент силы равен
, то момент силы равен 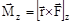 .
.
Момент импульса (количества движения) материальной точки А относительно неподвижной точки О есть векторная физическая величина, определяемая векторным произведением двух векторов: радиуса-вектора 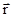 , проведенного из точки О в точку А, и импульса материальной точки
, проведенного из точки О в точку А, и импульса материальной точки 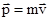
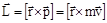 .
.
Направление вектора 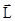 совпадает с направлением поступательного движения правого винта при его вращении от
совпадает с направлением поступательного движения правого винта при его вращении от 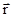 к
к 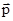 (рис.3.4).
(рис.3.4).
 Рис.3.4. Момент импульса относительно неподвижной точки.
Рис.3.4. Момент импульса относительно неподвижной точки.
|
Модуль вектора 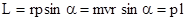 , a - угол между векторами
, a - угол между векторами 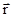 и
и 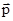 , l - плечо вектора
, l - плечо вектора 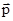 (или
(или  ) относительно точки О.
) относительно точки О.
Моментом импульса точки относительно неподвижной оси z называется скалярная величина Lz равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси 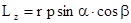 , где
, где 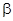 угол между вектором
угол между вектором 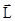 и осью z.
и осью z.
Момент импульса твердого тела есть векторная сумма моментов импульса всех точек, из которых состоит тело. Если число точек системы равно n, тогда 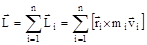 .
.
При вращательном движении твердого тела вокруг неподвижной оси угловые скорости w всех его точек равны, угол между векторами 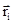 и
и 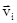 равен
равен 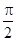 и все вектора
и все вектора 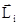 направлены по оси вращения в одну сторону. Отсюда модуль вектора
направлены по оси вращения в одну сторону. Отсюда модуль вектора 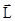 тела равен
тела равен 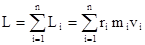 ,
, 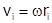 ,
,
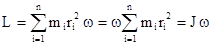 .
.
Момент импульса твердого тела, вращающегося вокруг неподвижной оси, равен произведению момента инерции этого тела относительно той же оси на угловую скорость.Направления векторов 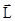 и
и 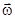 совпадают и
совпадают и 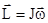 .
.
3. 2. Работа и кинетическая энергия при вращательном движении твердого тела. @
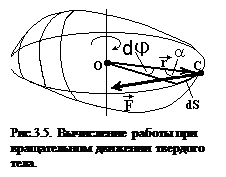
Найдем работу при вращательном движении твердого тела. Пусть ось вращения проходит через точку О, находящуюся на расстоянии r от точки приложения силы С, а a ‑ угол между векторами 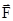 и
и 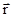 (рис.3.5). При повороте тела на бесконечно малый угол dj точка приложения силы проходит путь dS=rdj. Работа силы равна произведению проекции силы вдоль смещения Fsin(a) на величину этого смещения r dj .
(рис.3.5). При повороте тела на бесконечно малый угол dj точка приложения силы проходит путь dS=rdj. Работа силы равна произведению проекции силы вдоль смещения Fsin(a) на величину этого смещения r dj . 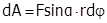 . Но F×r×sin(a ) = M - момент силы. Таким образом: работа силы при вращении тела вокруг неподвижной оси равна произведению момента действующей силы на угол поворота dA = Mdj.
. Но F×r×sin(a ) = M - момент силы. Таким образом: работа силы при вращении тела вокруг неподвижной оси равна произведению момента действующей силы на угол поворота dA = Mdj.
 Чтобы рассчитать кинетическую энергию вращательного движения твердого тела, мысленно его разобьем на n материальных точек с массами m1, m2,...,mn, находящихся на расстояниях r1, r2,...,rn от оси вращения. Так как тело абсолютно твердое, угловые скорости всех его точек одинаковы
Чтобы рассчитать кинетическую энергию вращательного движения твердого тела, мысленно его разобьем на n материальных точек с массами m1, m2,...,mn, находящихся на расстояниях r1, r2,...,rn от оси вращения. Так как тело абсолютно твердое, угловые скорости всех его точек одинаковы
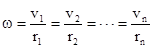 .
.
Линейные скорости точек будут разные 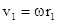 ,
, 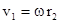 и т.д. Кинетическая энергия вращающегося тела Ек.вр равна
и т.д. Кинетическая энергия вращающегося тела Ек.вр равна
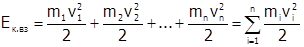 ;
;
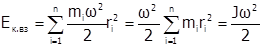 .
.
Работа внешних сил при вращении тела идет на увеличение его кинетической энергии. dA=dЕк.вр, следовательно работу можно представить как разность кинетических энергий конечного и начального положений
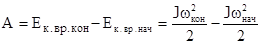
Если тело катится без скольжения, то оно одновременно участвует в двух движениях : поступательном и вращательном, и его кинетическая энергия
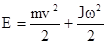 .
.
3. 3. Основное уравнение вращательного движения тела вокруг неподвижной оси. @
Воспользуемся соотношением, приведенным выше dA=dEвр, т.е.
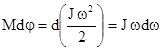
Поделим обе части равенства на dt:
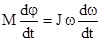 и так как
и так как 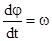 , а
, а 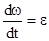 , то
, то 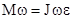 или
или 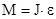
В векторном вид 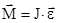 или
или 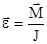 представляет собой уравнение динамики вращательного движения твердого тела вокруг неподвижной оси, проходящей через центр масс тела. Угловое ускорение, приобретаемое телом при вращении его вокруг неподвижной оси, прямо пропорционально вращающему моменту сил и обратно пропорционально моменту инерции тела. По форме оно сходно с уравнением II закона Ньютона. Из их сопоставления вытекает, что при вращательном движении роль массы играет момент инерции, роль линейного ускорения - угловое ускорение, роль силы - момент силы.
представляет собой уравнение динамики вращательного движения твердого тела вокруг неподвижной оси, проходящей через центр масс тела. Угловое ускорение, приобретаемое телом при вращении его вокруг неподвижной оси, прямо пропорционально вращающему моменту сил и обратно пропорционально моменту инерции тела. По форме оно сходно с уравнением II закона Ньютона. Из их сопоставления вытекает, что при вращательном движении роль массы играет момент инерции, роль линейного ускорения - угловое ускорение, роль силы - момент силы.
Ранее получено, что 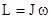 . Возьмем первую производную по времени от этого равенства
. Возьмем первую производную по времени от этого равенства
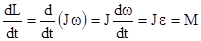 .
.
Это выражение есть вторая (более общая) форма уравнения динамики вращательного движения твердого тела: Скорость изменения момента импульса тела равна результирующему моменту всех внешних сил, (оно сходно с законом динамики поступательного движения: ).
Если на тело не действуют внешние силы или система тел замкнутая, то момент сил 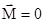 и
и  , откуда
, откуда 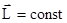 и получаем закон сохранения момента импульса: Момент импульса замкнутой системы тел остается постоянным во времени. Аналогом его в поступательном движении является закон сохранения импульса замкнутой системы тел. Закон сохранения момента импульса справедлив и для тел, размеры, форма и момент инерции которых могут меняться в ходе движения. Поскольку величина
и получаем закон сохранения момента импульса: Момент импульса замкнутой системы тел остается постоянным во времени. Аналогом его в поступательном движении является закон сохранения импульса замкнутой системы тел. Закон сохранения момента импульса справедлив и для тел, размеры, форма и момент инерции которых могут меняться в ходе движения. Поскольку величина 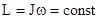 , то при увеличении момента инерции J, угловая скорость w уменьшается и наоборот. К примеру, акробат, совершая переворот в воздухе, чтобы увеличить угловую скорость своего вращения, группируется, т.е. прижимает к себе руки и ноги. При этом его момент инерции уменьшается.
, то при увеличении момента инерции J, угловая скорость w уменьшается и наоборот. К примеру, акробат, совершая переворот в воздухе, чтобы увеличить угловую скорость своего вращения, группируется, т.е. прижимает к себе руки и ноги. При этом его момент инерции уменьшается.
4. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ. @
4.1. Основные характеристики гармонического колебания. @
Колебательным движением называется процесс, при котором система многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему. Промежуток времени Т, спустя который процесс полностью повторяется, называется периодом колебания.
Колебательные движения широко распространены в природе и технике. Качание маятника часов, вибрация натянутой струны, морские приливы-отливы, тепловые колебания ионов кристаллической решетки твердого тела, переменный электрический ток, свет, звук. В зависимости от характера воздействия на колеблющуюся систему различают свободные незатухающие (или собственные) колебания, затухающие колебания, вынужденные колебания, автоколебания.
Свободные колебания происходят в системе, предоставленной самой себе после того, как она была выведена из положения равновесия. Простейшим свободным периодическим механическим колебанием является гармоническое колебательное движение точки (тела), при котором зависимость смещения из положения равновесия S от времени t описывается уравнениями:
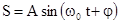 или
или 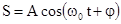 ,
,
А - амплитуда колебаний или максимальное смещение из положения равновесия, w0 - круговая (циклическая) частота, 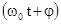 - фаза колебаний в момент времени t, j - начальная фаза колебаний или фаза в момент времени t=0. Такие колебания происходят под действием так называемых квазиупругих сил. Квазиупругие силы - это силы, имеющие такую же закономерность, как и сила упругости.
- фаза колебаний в момент времени t, j - начальная фаза колебаний или фаза в момент времени t=0. Такие колебания происходят под действием так называемых квазиупругих сил. Квазиупругие силы - это силы, имеющие такую же закономерность, как и сила упругости.
Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер близкий к гармоническим; 2) различные периодические процессы можно представить как сложение нескольких гармонических колебаний.
Через время Т фаза колебания получит приращение 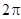 и колебательный процесс повторяется:
и колебательный процесс повторяется: 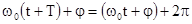 , откуда
, откуда 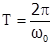 . Число полных колебаний в единицу времени есть частота колебаний n, для нее вытекают соотношения
. Число полных колебаний в единицу времени есть частота колебаний n, для нее вытекают соотношения 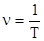 ,
, 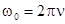 .Так как значения синуса и косинуса изменяются в пределах от +1 до -1, S принимает значения от +А до -А.
.Так как значения синуса и косинуса изменяются в пределах от +1 до -1, S принимает значения от +А до -А.
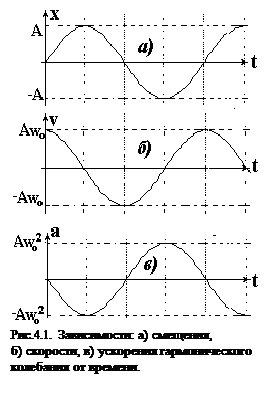
4.2. Скорость и ускорение при гармоническом колебании. @
Скорость гармонического колебания есть первая производная от смещения S по времени t. Пусть 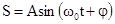 , тогда
, тогда
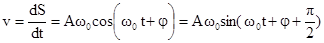 . Скорость сдвинута по фазе относительно смещения на p/2. Так как максимальное значение косинуса равно 1, максимальное значение скорости равно
. Скорость сдвинута по фазе относительно смещения на p/2. Так как максимальное значение косинуса равно 1, максимальное значение скорости равно 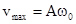 .
.
Ускорениеа гармонического колебания есть первая производная от скорости v по времени t.
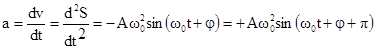 . Ускорение сдвинуто по фазе относительно смещения на p. Так как максимальное значение синуса равно 1, то максимальное значение модуля ускорения равно
. Ускорение сдвинуто по фазе относительно смещения на p. Так как максимальное значение синуса равно 1, то максимальное значение модуля ускорения равно 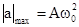 . На рис.4.1. представлены графики зависимости S, v и a от времени. Для удобства изображения начальная фаза принята равной нулю j=0, т.е.
. На рис.4.1. представлены графики зависимости S, v и a от времени. Для удобства изображения начальная фаза принята равной нулю j=0, т.е. 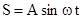 .
.
Связь ускорения и смещения можно получить, если в формуле для ускорения множитель 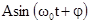 заменить на S, получим
заменить на S, получим 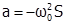 .
.
Сила, действующая на колеблющуюся материальную точку массой m по II закону Ньютона равна
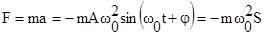 ,
, 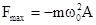 .
.
Отсюда следует, что сила пропорциональна смещению материальной точки и противоположна ему по направлению, такую силу называют квазиупругой. Согласно полученному выражению для силы можно сказать, что гармоническое колебание – это колебание, которое происходит при действии на тело квазигармонической силы.
Так как.  , то
, то  и
и 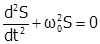 .
.
Полученное выражение называют дифференциальным уравнением гармонических колебаний, с точки зрения математики это линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его решениями являются: 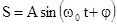 либо
либо 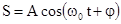 .
.
Кинетическая энергия материальной точки при гармоническом колебании равна
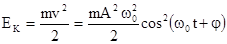
Потенциальная энергия материальной точки при гармоническом колебании под действием упругой силы, согласно ее определению, равна

Дата добавления: 2015-08-01; просмотров: 1294;
