Полная энергия колеблющейся точки

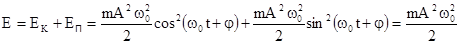
Полная энергия не зависит от времени. Следовательно, при гармонических ко­лебаниях выполняется закон сохранения механической энергии.

4. 3. Гармонический осциллятор. Примеры гармонических осцилляторов. @

Тела, которые при движении совершают гармонические ко­лебания, называют гармоническими осциляторами. Рассмотрим ряд примеров гармонических осциляторов.

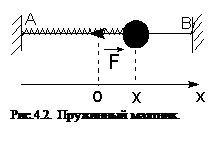
Пример1. Пружинный маятник – это тело массой m, способное совершать колебания под действием силы упругости невесомой (m_{пружины}<<m_тела) пружины (рис.4.2).

Трением в системе пренебрегаем. При смещении тела на расстояние х от положе­ния равновесия О на него дейст­вует сила уп­ругости пружины, направленная к положению равновесия: 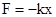, где k - коэффициент упругости (жесткости) пружины. По второму закону Ньютона 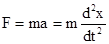. От­сюда 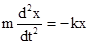и, если обозначить 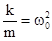, тогда получим 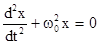дифференциальное урав­нение гармонических колебаний. Его решения имеют вид 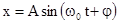либо 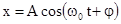. Таким образом, колебания пружинного маятника - гармонические с циклической час­тотой 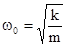и периодом .

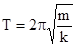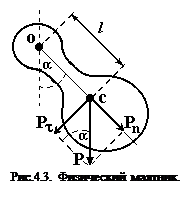
Пример 2. Физический маятник - это твердое тело, совер­шаю­щее колебания под действием силы тяжести вокруг подвижной го­ризон­тальной оси, не совпадающей с его цен­тром тяжести С (рис. 4. 3). Ось проходит через точку О. Если маятник откло­нить от положения равновесия на малый угол a и отпус­тить, он будет совершать ко­лебания, следуя основному уравнению динамики вращательного движения твердого тела 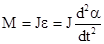, где J - момент инерции маятника относительно оси, М ‑ момент силы, возвращающей физический маятник в поло­жение равно­весия. Он создается силой тяжести 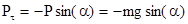, ее момент равен (l=ОС). В результате получаем 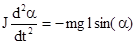. Это дифференциальное уравнение колебаний для произвольных углов отклонения. При малых углах, когда 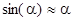, или, принимая 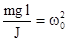, получим дифференциальное уравнение колебания физического маятника 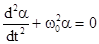. Его решения имеют вид 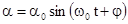или 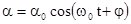. Таким образом, при малых отклонениях от положения равновесия физический маят­ник совершает гармонические колебания с циклической частотой 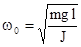и периодом .

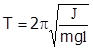Пример3. Математический маятник - это материальная точка с массой m (тяжелый шарик малых размеров), подвешенная на невесомой (по сравнению с m шарика), уп­ругой, нерастяжимой нити длинною l. Если вывести шарик из положения равновесия, отклонив его от вертикали на небольшой угол a, а затем отпустить, он будет совершать колебания. Если рассматривать данную систему как физический маятник с моментом инерции материальной точки J = ml², то из формул для физического маятника получим выражения для циклической частоты и периода колебаний математического маятника

, .

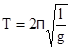4. 4. Затухающие колебания. @

В рассмотренных примерах гармонических колебаний единственной силой, действующей на материальную точку (тело), была квазиупругая сила F и не учитывались силы сопротивления, которые присутству­ют в лю­бой реальной системе. Поэтому рассмотренные колебания можно назвать идеальными незатухающими гармоническими колебаниями.

Наличие в реальной колебательной системе силы сопротивления среды при­во­дит к уменьшению энергии системы. Если убыль энергии не пополнять за счет работы внешних сил, колебания будут затухать. Затухающими называются колеба­ния с уменьшающейся во времени амплитудой.

Рассмотрим свободные затухающие колебания. При небольших скоростях сила сопротивления F_C пропорциональна скорости v и обратно пропорциональна ей по направлению 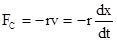, где r - коэффициент сопротивления среды. Используя второй закон Ньютона, получим дифференциальное уравнение затухающих колебаний 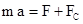, , 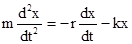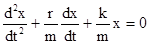. Обозначим 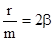, 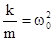. Тогда дифференциальное уравнение приобретает вид:

.

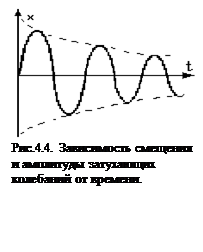
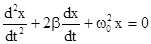Это дифференциальное уравнение затухающих колебаний. Здесь w₀ - собственная частота колеба­ний системы, т.е. частота свободных колебаний при r=0, b - коэффициент зату­хания оп­ределяет скорость убывания амплитуды. Решениями этого уравнения при условии b<w₀ являются

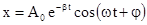либо .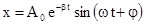

График последней функции представлен на рис.4.4. Верхняя пунктирная линия дает график функции 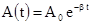, А₀ - амплитуда в начальный момент времени. Амплитуда во времени убывает по экспоненциальному закону, b - коэффициент зату­хания по величине обратен времени релакса­ции t, т.е. вре­мени за которое амплитуда уменьшается в e раз, так как

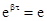, , bt = 1, 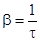. Частота и период затухающих колебаний 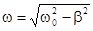, 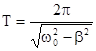; при очень малом сопротивлении среды (b²<<w₀²) период колебаний практически ра­вен 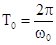. С ростом b период колебаний увеличивается и при b>w₀ решение дифференциального уравнения показывает, что колебания не совершаются, а происходит монотонное движение системы к положению равновесия. Такое движение называют апериодическим.

Для характеристики скорости затухания колебаний служат еще два параметра : декремент затухания D и логарифмический декремент l. Декремент затуха­ния показывает во сколько раз уменьшается амплитуда колебаний за время од­ного периода Т.

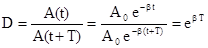
Натуральный логарифм от декремента затухания есть логарифмический декремент l

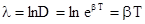. Так как 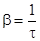, то 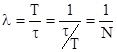, где N - число колебаний за время .

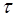4. 5. Вынужденные колебания. Механический резонанс. @

Если на колеблющуюся систему действует периодически изменяющаяся сила, то колебания называются вынужденными. Пусть вынуждающая сила изменяется по гармоническому закону
.

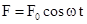Дифференциальное уравнение, получаемое из второго закона Ньютона, с учетом этой силы следует записать в виде

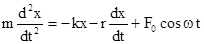или 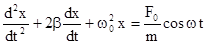. Решением дифференциального уравнения вынужденных колебаний является 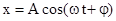, причем w - частота вынужденных колебаний совпадает с частотой колебания вынуждающей силы, а амплитуда вынужденных колебаний - А явля­ется сложной функцией от w и b.

.

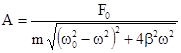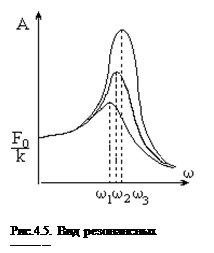
Зависимость ам­плитуды от w и b представлены на рис.4.5 (b₁>b₂>b₃). При w=0 все кри­вые сходятся в одной точке оси ординат 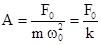. При различных значениях b амплитуд­ные кривые имеют максимумы, кото­рые со­ответст­вуют частотам w₁,w₂,...,w₀. Явление возрастания, а затем убывания амплитуды колеба­ний при изменении частоты на­звано механическим резонансом, а частоты w₁, w₂, ... , w₀, которым соот­ветст­вуют максимумы амплитуды, называют резонанс­ными часто­тами w_рез. Чтобы определить их значения, необ­ходимо найти максимум для функции амплиту­ды или, что то же самое, минимум подко­ренного выражения ( 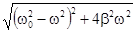). Продифференцировав подкоренное выражение по w и приравняв нулю, получим усло­вие, определя­ющее w_рез .

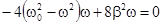Это уравнение имеет три решения: w=0 и ± 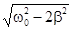. Физический смысл имеет лишь положительное значение. Следователь­но, резонансная частота w_рез= 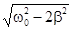, при b®0, w_рез®w₀. Если в формулу для амплитуды А подставить выражение w_рез= 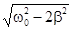, получим резонансное значе­ние А_рез .

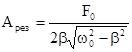Другая особенность вынужденных колебаний - это сдвиг фазы, а именно вы­ну­жденные колебания отстают по фазе на j от вынуждающей силы на величину j, ждя которой .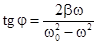

Величина сдвига фаз зависит от частоты w и коэффициента затухания b. Вынужден­ные колебания и вынуждающая сила имеют одинаковую фазу лишь при b=0, во всех реальных случаях b¹0 и j¹0. При w=w₀ для любых значений b сдвиг фазы равен 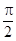, т.е. вынуждающая сила опережает по фазе вынужденные колебания на 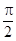. При w>>w₀ j®p, т.е. фазы силы и колебаний противоположны.

Явление механического резонанса необ­хо­димо учитывать при конструировании раз­лично­го рода сооружений : машин, кораблей, самолетов, мостов и др. Если, напри­мер, соб­ственная частота w₀ вибраций корпуса корабля или крыльев самолета сов­падает с частотой колебаний, возбуждаемых вращательным движением гребного винта или пропеллера возникнет механический резонанс, который может привести к разруше­нию. Однако явление резонанса имеет и положительное применение, например, в ра­диотехнике - для выделения нужного сигнала и множества других, отличаю­щихся по частоте, в акустике - для усиления звучания музыкального инструмента и т.д.

Для решения многих технических задач большой интерес представляют авто­колебания. Это незатухающие колебания в реальной колебательной системе, осу­ще­ствляемые под влиянием внешнего переменного воздействия, частота которого равна собственной частоте системы. В автоколебательной системе существует источник энергии, от которого периодически подается в систему энергия, компенсирующая ее убыль. Примером такой системы являются часы, где раскручи­вающая пружина или опускающиеся гирьки является источником энергии, а анкерное усройство под­талкивает маятник часов в такт к его колебаниями.

5. ВОЛНОВЫЕ ПРОЦЕССЫ @

5.1. Понятие о волнах. Виды волн. @

Если какую-либо частицу упругой среды заставить колебаться, то благодаря взаимодействию между частицами, соседние частицы тоже начнут колебаться, такой процесс вовлечения частиц в колебательное движение будет охватывать со временем все большее число частиц. Процесс рас­пространения колебаний в среде называется волновым процессом или волной. В таком процессе сами частицы среды не перемещаются на большие расстояния, они только совершают колебания около положений равновесия, причем частицы в разных точках ко­леблются с некоторым сдвигом по фазе.

Различают поперечные и продольные волны. Волна называется поперечной, если колебания частиц среды происходят в направлении, перпен­дикулярном к направлению распространения волны. Примеры поперечных волн: распространение колебаний атомов в узлах кристаллической решетки твердого тела, колебания величин электрического и магнитного полей при распространении электромагнитных волн, волны на поверхности воды и т.д. Волна называется продольной, если колебания частиц среды происходят около положений равновесия вдоль направления распространения волны. Примеры продольных волн: колебания в пружинных системах, распространение колебаний атомов в газах и жидкостях (распространение звуковых волн), такие колебания также возникают и в твердых телах.

Волны также делят по виду волновых поверхностей на плоские, сферические и др. Волновая поверхность ‑ это геометрическое место точек в пространстве, в которых колебания происходят одинаковым образом или в одной фазе. Для плоских волн волновые поверхности представляются параллельными плоскостями или линиями, для сферических волн – сферами или окружностями с общим центром (Рис.5.1). Волновые поверхности неподвижны. Поверх­ность, к которым подошли колебания в какой то момент времени и которая отделяет колеблющиеся частицы от ещё не ко­леблющихся частиц, называется фронтом волны.

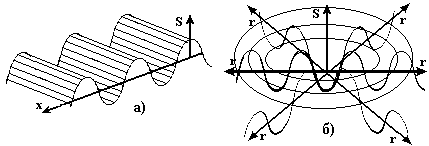
Рис.5.1.а) Плоская волна, б) Сферическая волна.

5.2. Волновое уравнение. Уравнения и характеристики волн.@

Если волна распространяется вдоль некоторого направления, то смещение частицы от положения равновесия S будет зависеть от времени t и от местоположения частицы х или r. Дифференциальное уравнение для волны имеет вид 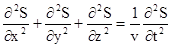и называется волновым уравнением, здесь v – скорость распространения волны. Решение такого уравнения имеет вид:

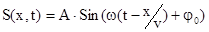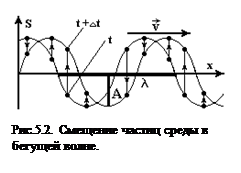
для плоской волны , а для сферической 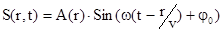. Графически такие волны изображают синусоидами, которые смещаются со временем (Рис.5.2), поэтому такие волны (в отличие от стоячих) называют бегущими волнами, хотя сами частицы вещества никуда не бегут, а колеблются около своего постоянного положения равновесия.

Новыми характеристиками, по сравнению с простыми колебаниями, являются фазовая скорость v, длина волны, волновое число. Фазовой скоростью или скоростью распространения волны v называют скорость перемещения фазы или точек пространства, где колебания находятся в одной фазе, например точек амплитудного значения А. Эта скорость равна скорости перемещения волнового фронта или скорости распространения волнового процесса. Длиной волны называют расстояние, на которое распространяется волновой процесс за время равное периоду колебаний Т (l = vT) или кратчайшее расстояние между частицами, колеблющихся в одной фазе. Используя эти характеристики, уравнения волн можно записать следующим образом:

для плоской волны 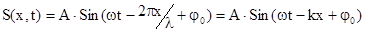, а для сферической волны 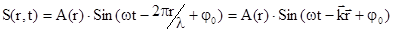, где k – волновое число, показывающее, сколько длин волн уложится на расстоянии в 2p метров (k = 2p/l = w/v), а 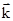‑ волновой вектор, равный по величине волновому числу и направленный вдоль вектора фазовой скорости.

5. 3. Энергия волны. Перенос энергии. @

Так как частицы среды двигаются при колебаниях и взаимодействуют между собой, то они обладают как кинетической, так и потенциальной энергией. В непрерывной среде рассматривают сумму кинетической и потенциальной энергии (механическую энергию) dE_м единицы объема dV вещества или объемную плотность энергии среды w_м = dЕ_м/dV. Расчет механической энергии приводит к выражению 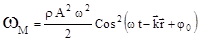, которое сходно с выражением для механической энергии колебаний осцилятора за исключением сомножителя 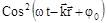, зависящего от времени. Это означает, что энергия в каждом объеме пространства меняется со временем за счет ее передачи от одной частицы к другой. Эксперименты показывают, что волны действительно переносят энергию, это относится как к механическим волнам в материальных средах, так и к электромагнитным волнам в вакууме. Процесс переноса энергии волной описывается вектором Умова‑Пойнтинга, который направлен вдоль вектора фазовой скорости и численно равен количеству переносимой энергии за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. Формула для его расчета имеет вид

.

Из этого выражения видно, что вектор Умова‑Пойнтинга тоже меняется со временем. Так как частоты реальных колебаний очень велики, то на практике обычно измеряются усредненные значения, для вектора Умова‑Пойнтинга среднее значение по времени от его модуля называют интенсивностью волнового процесса. Интенсивность волны I – это скалярная величина, показывающая количество переносимой волной энергии в среднем за единицу времени через единичную площадку, перпендикулярную к направлению движения волны. Если провести усреднение по времени одного полного колебания, то получим 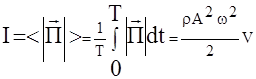. Отсюда видно, что интенсивность пропорциональна амплитуде колебаний. В случае плоской волны амплитуда и интенсивность не меняются по мере распространения волны, но для сферической волны А » 1/r и интенсивность убывает с расстоянием I » 1/r².

5. 4. Принцип суперпозиции волн. Явление интерференции.@

Если в среде распространяется одновременно несколько волн, то результирующие колебания частиц среды зависят от воздействия отдельных волн. В линейных средах выполняется принцип суперпозиции волн, согласно которому все параметры результирующего колебания (смещение, скорость, ускорение) равны сумме соответствующих параметров отдельных волн. Линейными являются все упругие среды, в которых смещения частиц от положения равновесия подчиняются закону Гука (смещение пропорционально силе, действующей на частицу). Нарушение принципа суперпозиции может происходить при распространении волн большой интенсивности. Например, при прохождении в среде лазерных лучей, такой большой мощности, что они могут изменить упругие свойства вещества, для результирующих колебаний этот принцип не соблюдается. Такие среды называют нелинейными.

В линейных средах, вследствие выполнения принципа суперпозиции, наблюдается явление интерференции света. Явление интерференции – это явление увеличения и уменьшения амплитуды результирующих колебаний при наложении двух или более когерентных волн, колеблющихся в одной плоскости. Когерентными называют волны, разница фаз которых не меняется со временем. Для объяснения этого явления рассмотрим случай наложения в точке М₁ или М₂ двух колебаний одной частоты, идущих от источников S₁ и S₂ (Рис.5.3).

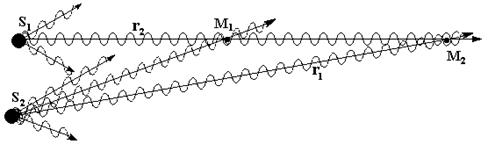
Рис.5.3. Сложение колебаний при интерференции (в точке М₁ – усиление, в точке М₂ – ослабление колебаний).

Уравнения волн в точке М будут иметь вид 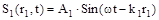и 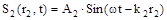. Суммарное колебание в точке М, используя формулу для синуса разности, можно представить в виде

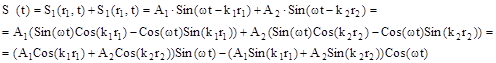
Последнее выражение можно рассматривать как 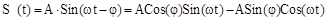, где

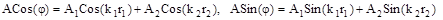. Из этих уравнений можно определить А и j . Разделив второе уравнение на первое находим 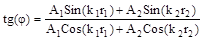, а возведя эти уравнения в квадрат и сложив их, можно найти что 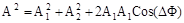, где разница фаз 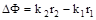. Если учесть, что интенсивность пропорциональна квадрату амплитуды колебаний, то после усреднения последнего уравнения получим .

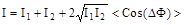В случае сложения не когерентных волн разница фаз меняется со временем произвольным образом и среднее значение косинуса будет равно нулю и 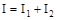, то есть происходит обычно наблюдаемое сложение интенсивностей колебаний. Но если колебания когерентные, то разница фаз не будет меняться со временем и среднее значение косинуса не будет равно нулю 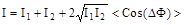. В этом случае в разных точках пространства будут различные значения суммарной амплитуды колебаний и интенсивности. В точках, для которых 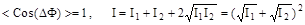и здесь будет максимальное усиление колебаний, в этих точках разница фаз должна быть равна - это условие для максимума интерференции. В точках, для которых 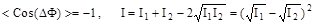и здесь будет максимальное ослабление колебаний, в этих точках разница фаз должна быть равна 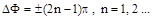- это условие для минимума интерференции. В точках, где не удовлетворяются эти условия, будут промежуточные значения амплитуды и интенсивности колебаний.

6. ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ. @

6.1. Преобразования Галилея и механический принцип относительности. @

В механике Ньютона при переходе от одной инерциальной системы отсчета к другой, движущейся относительно первой поступательно с постоянной скоростью, пользуются преобразованиями координат и времени, которые называются преобра­зованиями Галилея. Они основаны на двух аксиомах:

Ход времени одинаков во всех системах отсчета;