Это выражение является законом сохранения импульса. Суммарный импульс замкнутой системы точек (тел) не меняется с течением вре­мени.

Закон сохранения импульса находит широкое применение в природе и техни­ке. Примером может служить явление отдачи ружья при выстреле пули. Выстрел производится в горизонтальном направ­лении (рис.2.4).

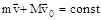Систему ружье-пуля можно считать изолированной системой и к ней приме­ним закон сохранения импульса: , m и v – масса и скорость пули, M и v₀ – масса и скорость ружья. В начальный момент времени (до выстрела) система покоилась (v=v₀=0), следовательно кон­стан­та в уравнении равна нулю. Отсюда, соотношение скоростей v и v₀ после выстрела, можно рассчитать из равенства , .

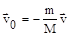Т.к. m<<M, то v>>v₀; знак «минус» указывает на противоположную направленность скоростей. Эксперименты доказывают, что закон сохранения импульса выполняется и для замкнутых систем микрочастиц, т.е. в квантовой механике. Таким образом, закон сохранения импульса универсален и является фунда­ментальным законом природы.

2. 4. Центр масс. Закон движения центра масс. @

Центр масс (или центр инерции) системы материальных точек (тел) есть некоторая точка в пространстве С, положение которой характеризует распределение масс сис­темы. Ее радиус-вектор равен : , где n – число точек (тел) системы, m₁, m₂…m_n – их массы; 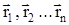- их радиусы-векторы; m – общая масса систе­мы.Ско­рость центра масс

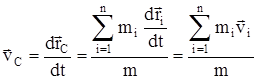. Так как 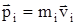, 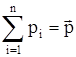- импульс всей системы, то 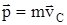или импульс системы равен произведению массы системы на скорость ее центра масс.

По II за­кону Ньютона 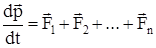. Отсюда , т.е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на нее действует сила, равная геометрической сумме всех внешних сил, действующих на тела системы. Это есть закон движения центра масс. Если система замкнута, то , 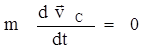и .

Следовательно центр масс замкнутой системы движется прямолинейно и рав­номерно, либо остается неподвижным. Например, молоток вращается, а его центр масс движется прямолинейно и равномерно (рис.2.5).

Рис.2.5. Свободно летящий молоток. Его центр инерции помечен крестиком.

2. 5. Принцип реактивного движения. Уравнение движения тела с переменной массой. @

Особый интерес представляет применение закона сохранения импульса к яв­лению «непрерывной отдачи», происходящему в реактивном двигателе (ракете). Если рассматривать ракету и выбра­сываемые ею продукты сгорания как единую ме­ханическую систему, то для полу­чения уравнения ее движения можно применить закон сохранения импульса. Эта идея была высказана в 1881 г. Н.И.Кибальчичем и разви­та в трудах К.Э.Циолковского. Уравнение движения тела с переменной массой было выведено в 1897г. И.В.Мещерским.

При выводе уравнения необходимо учитывать, что в процессе движения ракеты изменяется ее масса, т.к. уда­ляются продукты сгорания. Пусть в момент времени t масса ракеты – m и ее скорость - 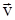. Через интервал времени dt масса ее уменьшится на dm и станет равной m-dm, а скорость будет равна . Образовавшиеся продукты сгорания топлива за время dt приобрели импульс , где - скорость истечения газа относительно ракеты. Изменение им­пульса всей системы (ракета + продукты сгорания) за время dt равно

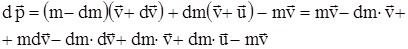
Так как 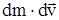- пренебрежимо малая величина, поэтому после сокращений получим . Полагая, что на ракету в далеком космосе не действуют внешние силы, то из закона сохранения импульса следует, что .

Разделим обе части равенства на dt и после простых преобразований получим .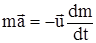

Выражение в правой части равенства имеет размерность силы и называется реактивной си­лой . Таким образом уравнение динамики движения ракеты в космосе можно за­писать в виде: . Интегрируя обе части этого равенства, получим . Постоянную интегрирования С находим из начальных условий : в мо­мент времени t=0 скорость ракеты v=0 и масса m=m₀, тогда и .

Эта формула называется формулой Циолковского. Скорость ракеты v будет тем больше, чем больше масса ракеты и скорость истечения продуктов сго­рания то­плива.

Если на систему действуют внешние силы 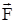, то и аналогичным образом плучается уравнение И.В.Мещерского в виде :

2.6. Энергия, работа, мощность. @

Одного понятия импульса оказалось недостаточно для характеристики движения. Например, два снаряда с массами m₁=1кг, m₂=10кг и скоростями v₁=10м/c, v₂=1м/c имеют одинаковые импульс р=10кг×м/с, но их разрушающее действие для преграды будет совершенно разное (у первого в 10 раз больше).

Единой мерой различных форм движения и взаимодействия всех видов мате­рии яв­ляется энергия. Различным видам движения и взаимодействия материи, соответствуют различные виды энергии: механическая, те­пловая, химическая, электро-магнитная, атомная.

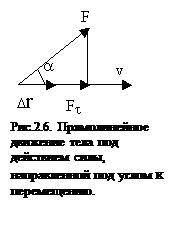
Простейшей форме движения – меха­нической, соответствует меха­ни­ческая энергия. Она характеризует способность тела или системы тел совершать работу и измеряется количе­ством работы, ко­торую при опре­деленных (заданных) условиях может совершить система. На­пример, катя­щийся шар, сталкиваясь с неко­торым телом, перемещает его, т.е. со­вершает работу. Растянутая пружина, со­кра­ща­ясь после устранения дефор­мирующей силы, совер­шает работу по перемещению своих частей (витков). Следователь­но, катящийся шар и растянутая пружина обла­дают механической энергией.Про­цесс изменения механической энер­гии тела под действием силы называется процес­сом совершения работы. Прираще­ние энергии тела в этом процессе называется работой силы, отсюда следует общее соотношение, связывающее работу и изменение энергии

А=Е₂-Е₁,