Кинематика изучает движение тел, не рассматривая причины, вызывающие это движение.
1.1. Система отсчета. Радиус‑вектор материальной точки.@
Простейшим примером механического движения является движение материальной точки. Материальная точка – это модель реального тела, размерами которого в данной задаче можно пренебречь. Для описания механического движения необходимо ввести тело отсчета и систему отсчета.
 Тело отсчета – это тело, условно принятое за неподвижное. Система отсчета – совокупность системы координат и часов, связанных с телом отсчета. Для решения большинства физических задач систему отсчета связывают либо с Солнцем, либо с Землей. Система отсчета, центр которой совмещен с Солнцем, называется гелиоцентрической (гелиос - по-гречески Солнце). Система отсчета, центр которой совмещен с Землей называется геоцентрической (геос - по-гречески Земля). Правильный выбор системы координат часто упрощает решение поставленной физической задачи. Важнейшими пространственными системами координат, применяемых в механике, являются прямоугольная декартова и системы криволинейных координат (цилиндрическая, сферическая, эллипсоидная и др.).
Тело отсчета – это тело, условно принятое за неподвижное. Система отсчета – совокупность системы координат и часов, связанных с телом отсчета. Для решения большинства физических задач систему отсчета связывают либо с Солнцем, либо с Землей. Система отсчета, центр которой совмещен с Солнцем, называется гелиоцентрической (гелиос - по-гречески Солнце). Система отсчета, центр которой совмещен с Землей называется геоцентрической (геос - по-гречески Земля). Правильный выбор системы координат часто упрощает решение поставленной физической задачи. Важнейшими пространственными системами координат, применяемых в механике, являются прямоугольная декартова и системы криволинейных координат (цилиндрическая, сферическая, эллипсоидная и др.).
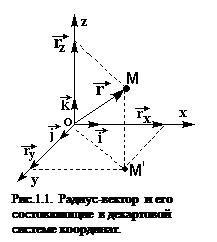
Пусть точка М движется в пространстве. На рис.1.1 представлены тело отсчета О и связанная с ним прямоугольная декартова система координат. Вектор, соединяющий начало (тело) отсчета с точкой М, есть радиус-вектор этой точки 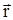 . Из точки М опустим перпендикуляры на ось OZ и плоскость ХОY. Из точки М’ проведем перпендикуляры к осям ОХ и OY.Векторы
. Из точки М опустим перпендикуляры на ось OZ и плоскость ХОY. Из точки М’ проведем перпендикуляры к осям ОХ и OY.Векторы 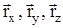 на координатных осях называются составляющими радиуса-вектора. Пользуясь правилом сложения векторов можно получить
на координатных осях называются составляющими радиуса-вектора. Пользуясь правилом сложения векторов можно получить 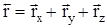
Модули 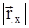 ,
, 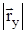 ,
, 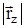 есть проекции радиуса-вектора на координатные оси. Проекция – всегда скалярная величина. Эти проекции называются координатами материальной точки М – x, y, z . Отсюда
есть проекции радиуса-вектора на координатные оси. Проекция – всегда скалярная величина. Эти проекции называются координатами материальной точки М – x, y, z . Отсюда 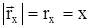 ,
, 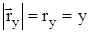 ,
, 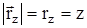 .
.
Каждому вектору может быть сопоставлен единичный вектор (орт), имеющий то же направление, что и сам вектор, но по модулю равный единице. Пусть 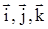 - орты координатных осей соответственно. Тогда можно записать
- орты координатных осей соответственно. Тогда можно записать 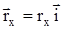 ,
, 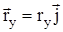 ,
, 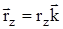 или
или 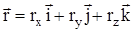 .
.
При движении материальной точки ее координаты и радиус-вектор изменяются с течением времени. Поэтому в общем случае можно записать: 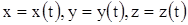 или
или  .
.
Это уравнение называется кинематическим уравнением движения материальной точки. Непрерывная кривая, которую описывает точка при своем движении относительно системы координат, называется траекторией.
1.2. Кинематические характеристики и уравнения поступательного движения. @
Кроме модели реального тела в виде материальной точки, в физике часто используется модель абсолютно твердого тела. Тело считается абсолютно твердым, если в условиях рассматриваемой задачи оно не деформируется, т.е. расстояние между любыми двумя произвольными точками сохраняется неизменным.
Движение материальной точки и твердого тела можно разложить на два вида движения - поступательное и вращательное. Любой другой вид движения есть их комбинация.
Поступательное движение твердого тела - это такое движение, при котором любая прямая,  жестко связанная с телом, остается параллельной самой себе (рис.2.1). Поступательное движение твердого тела будет прямолинейным, если траектории всех его точек - параллельные прямые линии; криволинейным, если траектории произвольной формы.
жестко связанная с телом, остается параллельной самой себе (рис.2.1). Поступательное движение твердого тела будет прямолинейным, если траектории всех его точек - параллельные прямые линии; криволинейным, если траектории произвольной формы.
Пусть за время 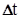 материальная точка переместилась из положения А в В по криволинейной траектории (рис.3.1). Расстояние, пройденное точкой вдоль траектории за время
материальная точка переместилась из положения А в В по криволинейной траектории (рис.3.1). Расстояние, пройденное точкой вдоль траектории за время 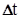 есть скалярная, положительная величина – путь
есть скалярная, положительная величина – путь 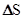 .
. 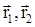 - радиусы-векторы точек А и В.
- радиусы-векторы точек А и В.
Вектор, соединяющий точки А и В, называется вектором перемещения  ,
, 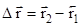 . В общем случае модуль вектора перемещения не равен пути (см. рис.3.1)
. В общем случае модуль вектора перемещения не равен пути (см. рис.3.1) 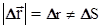 . Лишь при прямолинейном движении
. Лишь при прямолинейном движении 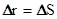 . На малых временных интервалах, когда
. На малых временных интервалах, когда 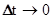 , можно с большой точностью считать, что
, можно с большой точностью считать, что 
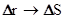 .
.
Векторная физическая величина, характеризующая изменение радиус-вектора с течением времени, называется скоростью. Скорость характеризует изменение 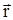 как по численному значению, так и по направлению. Различают среднюю и мгновенную скорости. Средняя скорость
как по численному значению, так и по направлению. Различают среднюю и мгновенную скорости. Средняя скорость 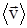 - это скорость за данный промежуток времени на данном участке траектории. Она равна отношению вектора перемещения
- это скорость за данный промежуток времени на данном участке траектории. Она равна отношению вектора перемещения 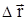 за время
за время  к этому промежутку времени
к этому промежутку времени 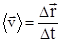 . Мгновенная скорость
. Мгновенная скорость 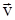 - это скорость в данный момент времени, в данном месте траектории. Она определяется как предел, к которому стремится
- это скорость в данный момент времени, в данном месте траектории. Она определяется как предел, к которому стремится 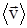 при
при  ®0. Отсюда следует
®0. Отсюда следует 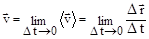 .
.
Математически, вектор мгновенной скорости равен первой производной от радиуса-вектора по времени.Таким образом 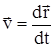 . Вектор
. Вектор 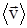 направлен вдоль вектора
направлен вдоль вектора 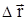 , вектор
, вектор 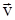 направлен по касательной к траектории в данной точке.
направлен по касательной к траектории в данной точке.
Векторная физическая величина, характеризующая изменение вектора скорости с течением времени называется ускорением 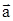 . Различают среднее и мгновенное ускорения. Среднее ускорение
. Различают среднее и мгновенное ускорения. Среднее ускорение 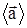 равно отношению изменения вектора скорости за время Dt к этому промежутку времени
равно отношению изменения вектора скорости за время Dt к этому промежутку времени 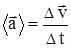 . Мгновенное ускорение
. Мгновенное ускорение 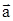 , т.е. ускорение в данный момент времени находится как предел
, т.е. ускорение в данный момент времени находится как предел 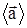 при Dt ®0. Отсюда
при Dt ®0. Отсюда 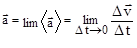 =
= 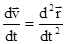 .
.
Дата добавления: 2015-08-01; просмотров: 2119;
