Теорема о сложении скоростей

Теорема. При сложном (составном) движении точки ее абсолютная скорость υ_a равна векторной сумме отно­сительной υ_r и переносной υ_е скоростей.

Пусть точка М совершает одновременные движения по отношению к неподвижной и подвижной системам координат (рис. 56). Обозначим угловую скорость поворота системы коор­динат Оξηζ через ω. Положение точки М определяется радиусом-вектором r.

Установим соотношение между скоростями точки М по отноше­нию к двум системам координат — неподвижной и подвижной. На основании доказанной в предыдущем параграфе теоремы

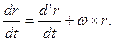
Из кинематики точки известно, что первая производная от ра­диуса-вектора движущейся точки по времени выражает скорость этой точки. Поэтому 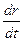= r = υ_а — абсолютная скорость, 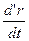=υ_r — относительная скорость,

а ω x r = υ_е — переносная ско­рость точки М. Следовательно,

υ_а= υ_r+ υ_е

Формула (11.79) выражает правило параллелограмма скоростей. Модуль абсолютной скорости найдем по теореме косинусов:

υ_a=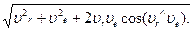

В некоторых задачах кинематики требуется определить относи­тельную скорость υ_r. Из (11.79) следует

υ_r= υ_а+( - υ_е ).

Таким образом, чтобы построить вектор относительной скорости, нужно геометрически сложить абсолютную скорость с век­тором, равным по абсолютной величине, но противоположно направ­ленным переносной скорости.