Дивергенция вектора. Теорема Остроградского–Гаусса

Пусть задано векторное поле 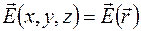. Возьмем некоторую точку 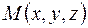и произвольную замкнутую поверхность 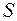, окружающую эту точку. Найдем поток вектора 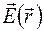через эту поверхность:

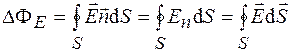. (33.1)

Величина потока зависит как от характеристик поля 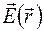, так и от размеров и формы поверхности S. Пусть объем, ограниченный поверхностью S, равен 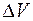. Составим отношение

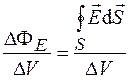(33.2)

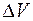и будем стягивать поверхность S в точку М таким образом, чтобы объем стремился к нулю, а точка М оставалась внутри поверхности (рис. 33.1). Предел отношения потока вектора 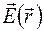через произвольную замкнутую поверхность 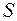, окружающую точку 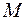, к объему 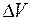, ограниченному этой поверхностью, когда поверхность 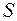стягиваетсяв точку М, называется дивергенцией 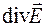вектора 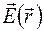в точке :

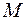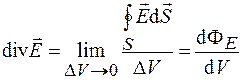. (33.3)

Из определения следует, что дивергенция вектора есть скалярная величина. Если вектор 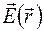задан своими проекциями в декартовой системе координат, каждая из которых в общем случае зависит от всех трех координат: 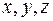, т. е. 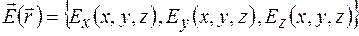, то дивергенция вектора

. (33.4)

В математике доказывается теорема Остроградского–Гаусса, согласно которой поток вектора 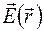через произвольную замкнутую поверхность 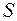равен интегралу от дивергенции вектора 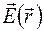по объему 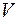, ограниченному этой поверхностью, т. е.

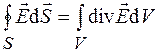. (33.5)

Теорема Остроградского–Гаусса допускает наглядное гидродинамическое истолкование. Пусть вектор 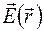– это вектор скорости течения несжимаемой жидкости, т. е. 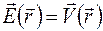. Тогда поток вектора 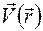через замкнутую поверхность S будет равен разности количества жидкости, вытекающей из объема 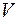, и количества жидкости, втекающей в этот же объем, в единицу времени. Если внутри поверхности 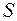отсутствуют источники (или стоки) жидкости, то количество вытекающей жидкости будет в точности равно количеству втекающей жидкости и поток вектора скорости будет равен нулю. Этот же вывод следует из того, что при отсутствии источников жидкости линии тока жидкости будут непрерывны в объеме 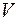и количество линий тока, выходящих из объема 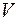, будет равно количеству линий тока, входящих в этот объем.

Если внутри поверхности S имеются источники жидкости, то количество вытекающей и втекающей в единицу времени жидкости окажется различным, поток вектора скорости через замкнутую поверхность S будут отличен от нуля, а его величина будет равна количеству жидкости, "вырабатываемой" источниками в единицу времени. Теорема Остроградского–Гаусса утверждает, что этот поток будет равен интегралу по объему V от дивергенции вектора скорости. Но тогда дивергенция вектора характеризует объемную плотность источников жидкости, т. е. количество жидкости, "вырабатываемой" в единице объема.

Таким образом, можно сделать вывод, что если внутри замкнутой поверхности имеются источники поля вектора 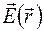, то поток вектора 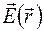через эту поверхность отличен от нуля, а величина дивергенции вектора 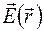характеризует объемную плотность источников поля.