Векторы в науке и технике. Понятие вектора. Координаты вектора
В физике и математике вектор – это величина, которая характеризуется численным значением и направлением. В физике встречается немало важных величин, которые характеризуются направлением. Например, сила, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким как масса, объем, давление, температура, плотность, которые можно описать обычным числом и называются они скалярными величинами.
Векторная запись используется при работе с величинами, которые невозможно задать полностью с помощью обычных чисел. Например, необходимо описать положение предмета, но полностью определить местоположение предмета невозможно, пока не будет известно направление, в котором он находится. Таким образом, местонахождение предмета характеризуется численным значением (расстоянием в километрах) и направлением.
При изучении и расчете цепей переменного тока удобно пользоваться векторными диаграммами, на которых синусоидальные напряжения и токи условно изображают с помощью векторов. Применение этих диаграмм упрощает изучение и расчет цепей и вносит наглядность в рассматриваемые соотношения.
Вектором на плоскости называется направленный отрезок 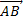 с начальной точкой
с начальной точкой  и конечной точкой
и конечной точкой 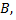 который можно перемещать параллельно самому себе.
который можно перемещать параллельно самому себе.


Рис. 1
Вектор на плоскости
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос. При параллельном переносе точки смещаются по параллельным или совпадающим прямым на одно и тоже расстояние.
Нулевой вектор – точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.
Абсолютной величиной или модулем вектора называется длина отрезка, изображающего вектор. Другими словами длина вектора есть расстояние между началом и концом вектора
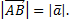
Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых. Нулевой вектор коллинеарен любому вектору. Если векторы 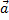 и
и 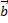 коллинеарны и их лучи сонаправлены, то векторы
коллинеарны и их лучи сонаправлены, то векторы 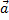 и
и 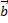 называют сонаправленными. Обозначают
называют сонаправленными. Обозначают 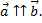 Если векторы
Если векторы 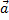 и
и 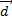 коллинеарны, а их лучи не являются сонаправленными, то векторы называют противоположно направленными. Обозначают
коллинеарны, а их лучи не являются сонаправленными, то векторы называют противоположно направленными. Обозначают  Нулевой вектор условились считать сонаправленным с любым вектором.
Нулевой вектор условились считать сонаправленным с любым вектором.

Рис.2
Коллинеарные вектора
Свойство коллинеарных векторов.
Если векторы 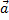 и
и 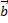 коллинеарны и
коллинеарны и 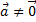 , то существует число
, то существует число 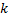 такое, что
такое, что 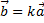 . Причем, если
. Причем, если 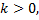 то векторы
то векторы 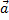 и
и 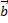 сонаправленные, если
сонаправленные, если 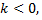 то противоположно направленные.
то противоположно направленные.
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Признак компланарности трех векторов.
Если вектор 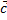 можно разложить по векторам
можно разложить по векторам 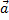 и
и 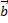 , т.е. представить в виде
, т.е. представить в виде 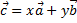 , где
, где 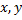 -некоторые числа, то векторы
-некоторые числа, то векторы 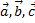 -компланарны.
-компланарны.

Рис.3
Компланарные вектора
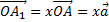 , где
, где 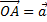 ;
;
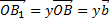 , где
, где 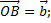
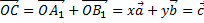 , где
, где 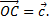
Дата добавления: 2015-08-11; просмотров: 2630;
