Скалярное произведение векторов, основные свойства и выражение в координатной форме
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними 
Формулу для скалярного произведения векторов можно записать в виде
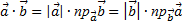 .
.
Скалярное произведение двух векторов равно модулю одного из них, помноженному на алгебраическую проекцию другого вектора на направление первого.
Скалярное умножение нельзя распространить на случай трех сомножителей. Действительно, скалярное произведение двух векторов 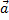 и
и 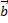 есть число и если это число умножить на вектор
есть число и если это число умножить на вектор 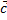 , то в произведении получим вектор
, то в произведении получим вектор
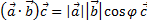
коллинеарный с вектором 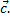
Свойства скалярного произведения векторов:

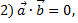 если
если 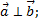
3) 
4) 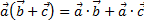 ;
;
5) 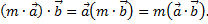
Если рассматривать векторы 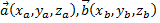 в декартовой системе координат, то скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов
в декартовой системе координат, то скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов
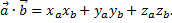
Используя полученное равенство, можно записать формулу для вычисления угла между векторами
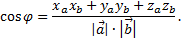
Рассмотрим пример. Найти 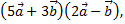 если
если 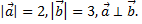
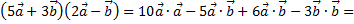
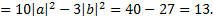
Так как 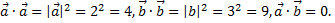
Рассмотрим пример. Найти угол между векторами 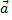 и
и 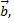 если
если 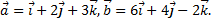



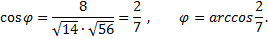
Рассмотрим пример. Найти скалярное произведение
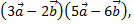 если
если 
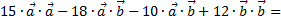
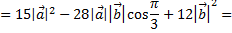

Дата добавления: 2015-08-11; просмотров: 1237;
