Смешанное произведение векторов. Основные свойства смешанного произведения векторов и выражение в координатной форме
Смешанное произведение векторов.
Смешанным произведением векторов 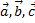 называется скалярное произведение вектора
называется скалярное произведение вектора 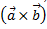 на вектор
на вектор 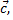 т.е.
т.е.
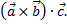
Обращение в нуль смешанного произведения векторов 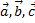 есть признак компланарности векторов
есть признак компланарности векторов 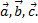
Смешанное произведение трех векторов 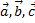 по модулю равно объему параллепипеда, построенного на этих векторах.
по модулю равно объему параллепипеда, построенного на этих векторах.
Свойства смешанного произведения трех векторов.
1. При круговой перестановке сомножителей смешанное произведение не меняется, при перестановке двух сомножителей – меняет знак на обратный

2. Свойство распределительности 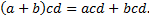
3. Свойство сочетательности относительно скалярного множителя 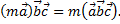
4. Смешанное произведение, имеющее хотя бы два равных сомножителя, равно нулю 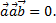
Пусть векторы заданы их разложениями по ортам
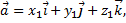
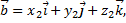
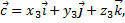
тогда смешанное произведение векторов
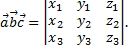
Дата добавления: 2015-08-11; просмотров: 894;
