Векторное произведение векторов. Основные свойства векторного произведения векторов и выражение в координатной форме
Векторное произведение векторов 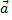 и
и 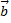 называется вектор
называется вектор 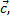 удовлетворяющий следующим условиям:
удовлетворяющий следующим условиям:
1) модуль вектора  равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах 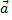 и
и 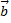
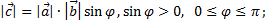
2) направление вектора  перпендикулярно плоскости параллелограмма построенного на векторах
перпендикулярно плоскости параллелограмма построенного на векторах 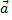 и
и 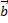 ;
;
3) векторы 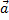 ,
, 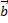 и
и  после приведения к общему началу ориентированы по отношению друг к другу соответственно как орты
после приведения к общему началу ориентированы по отношению друг к другу соответственно как орты 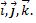
Свойства векторного произведения векторов.
1) Векторное произведение не обладает переместительным свойством 
2) Коллинеарность ненулевых векторов 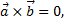 если
если
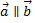 или
или 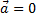 или
или 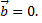
3) Сочетательное свойство

4) Распределительное свойство
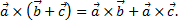
Если заданы векторы 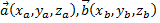 в декартовой системе координат, то их векторное произведение находят следующим образом
в декартовой системе координат, то их векторное произведение находят следующим образом
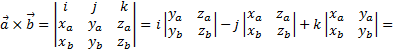
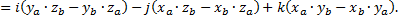
Рассмотрим пример. Найти векторное произведение двух векторов 
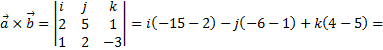

Дата добавления: 2015-08-11; просмотров: 1109;
