Декартова система координат
Декартова система координат в пространстве определяется заданием линейной единицы для измерения длин и трех пересекающихся в одной точке взаимно перпендикулярных осей. Точка пересечения осей называется началом координат, а сами оси – координатными осями. Первая координатная ось называется осью абсцисс, вторая – осью ординат, а третья – осью аппликат. Начало координат обозначается буквой 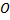 , координатные оси соответственно символами –
, координатные оси соответственно символами – 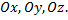 Отложив на осях
Отложив на осях 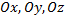 в положительном направлении отрезки равные единице масштаба, получим три основных вектора
в положительном направлении отрезки равные единице масштаба, получим три основных вектора 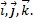
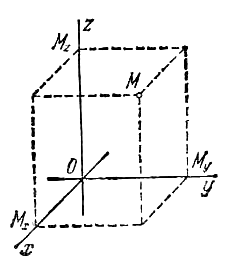
Рис.9
Декартова система координат в пространстве
Пусть 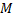 -произвольная точка пространства,
-произвольная точка пространства, 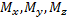 -ее проекции на координатные оси. Координатами точки
-ее проекции на координатные оси. Координатами точки 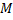 в заданной системе называются числа
в заданной системе называются числа 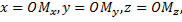 где
где 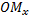 - величина отрезка
- величина отрезка 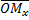 оси абсцисс,
оси абсцисс, 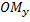 - величина отрезка
- величина отрезка 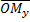 оси ординат,
оси ординат, 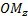 - величина отрезка
- величина отрезка 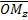 оси аппликат. Число
оси аппликат. Число  называется абсциссой, y-ординатой, -апликатой точки
называется абсциссой, y-ординатой, -апликатой точки 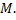 Символ
Символ 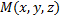 обозначает, что точка
обозначает, что точка 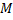 имеет координаты
имеет координаты 
Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала. Если заданы точки

то
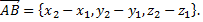
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве 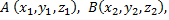 то
то
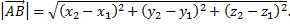
Если точка 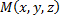 делит отрезок
делит отрезок 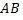 в соотношении
в соотношении 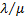 от
от  то координаты этой точки определяются так:
то координаты этой точки определяются так:
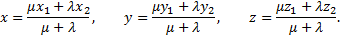
В частном случае координаты середины отрезка находятся как
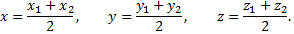
Линейные операции над векторами в координатах.
Пусть заданы векторы 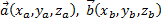 тогда
тогда
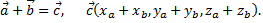
Расстояние между двумя точками определяется по формуле
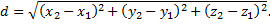
Рассмотрим пример. Даны точки  на прямой
на прямой 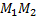 найти точку
найти точку 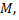 делящую отрезок
делящую отрезок 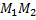 в отношении
в отношении 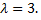

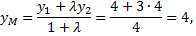
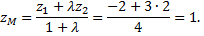
Следовательно, 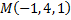 - искомая точка.
- искомая точка.
Рассмотрим пример. На оси 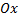 найти точку, равноудаленную от точек
найти точку, равноудаленную от точек 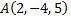 и
и 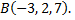
Должно выполняться равенство 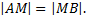 Так как точка
Так как точка 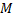 лежит на оси
лежит на оси 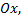 то ее координаты
то ее координаты 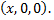 Тогда
Тогда
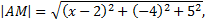
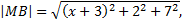
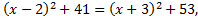
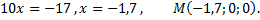
Дата добавления: 2015-08-11; просмотров: 1458;
