Однородные системы линейных алгебраических уравнений

Система 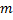линейных уравнений с 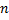переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю.

Системы линейных однородных уравнений:

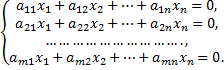
Система линейных однородных уравнений всегда совместна, так как имеет, по крайней мере, нулевое решение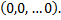

Если в однородной системе 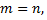а ее определитель отличен от нуля, то такая система имеет только нулевое решение.

Система линейных однородных уравнений имеет ненулевое решение тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при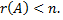

Рассмотрим пример. Найти решение системы линейных алгебраических уравнений

Составим по данной системе расширенную матрицу

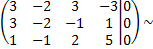
поменяем местами первую и третью строки

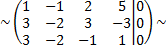
умножим первую строку на 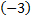и сложим со второй строкой, а затем с третьей строкой, получим

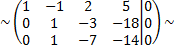
умножим вторую строку на 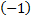и сложим с третьей строкой

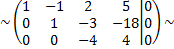
разделим последнюю строку на

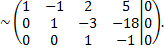
Таким образом, ранг расширенной матрицы и ранг основной матрицы равны 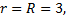следовательно, система совместна. Число строк в основной матрице равно 3, а число столбцов равно 4, т.е. решений множество. Определим базисные переменные

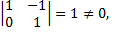
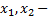базисные переменные.

Перейдем от матрицы к системе, выразим переменные 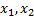через другие переменные

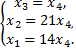
Контрольные вопросы

1. Сформулировать теорему Кронекера – Капелли.

2. Сформулировать Метод Гаусса решения систем m линейных уравнений с n неизвестными.

3. Дать определение базисному решению систем линейных алгебраических уравнений.

4. Какие системы линейных алгебраических уравнений называют однородными?