Теорема Кронекера-Капелли

Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы равен рангу расширенной матрицы этой системы.

Для совместных систем линейных уравнений верны следующие теоремы.

1) Если ранг матрицы совместной системы равен числу переменных, т.е. 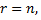то система имеет единственное решение.

2) Если ранг матрицы совместной системы меньше числа переменных, т.е. 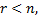то система неопределенная и имеет бесконечное множество решений.

3.2. Метод Гаусса решения систем m линейных уравнений с n неизвестными

Метод Гаусса – метод последовательного исключения переменных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Шаг первый. Умножая первое уравнение на подходящие числа

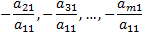
и прибавляя полученные уравнения соответственно ко второму, третьему, …, 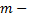му уравнению системы, исключим переменную 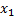из всех последующих уравнений, начиная со второго. Получим

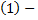обозначены новые коэффициенты, полученные после первого шага.

Шаг 2. Пусть 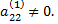Умножая второе уравнение на подходящие числа

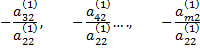
и прибавляя полученные уравнения соответственно к третьему, четвертому, 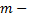му уравнению системы, исключим переменную из всех последующих уравнений, начиная с третьего.

Последующие шаги проводятся аналогично.

Процесс последовательного исключения переменных после 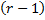-го шага приводит к системе

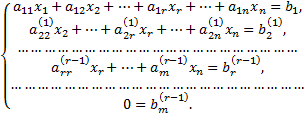
Если хотя бы одно из чисел 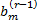не равно нулю, то соответствующее равенство противоречиво, и система несовместна. Для любой совместной системы числа 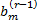в системе равны нулю.

После отбрасывания «лишних» уравнений возможны два случая:

а) число уравнений системы, приведенной к ступенчатому виду равно числу переменных, т.е. ;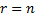

б) число уравнений системы, приведенной к ступенчатому виду меньше числа переменных .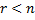

Переход системы к равносильной ей системе называется прямым ходом метода Гаусса, а нахождение переменных из равносильной системы – обратным ходом.

Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов.

Рассмотрим пример. Решить систему уравнений методом Гаусса

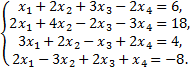
Составим по данной системе расширенную матрицу

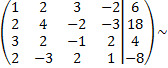
умножим первую строку на 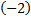и сложим со второй строкой и с четвертой строкой; умножим первую строку на и сложим с третьей строкой, получим

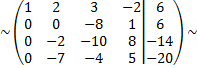
поменяем местами вторую и третью строки

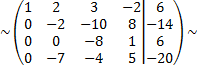
умножим вторую строку на 7 и сложим с четвертой строкой

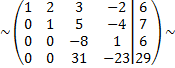
умножим третью строку на 31, а четвертую на 8 и сложим эти строки

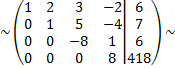
разделим последнюю строку на 2

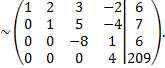
От ступенчатого вида матрицы переходим к системе

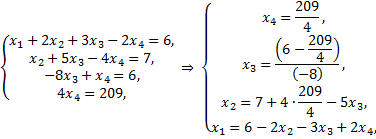
т.е. обратным ходом Гаусса находим все переменные.

Рассмотрим пример. Решить систему методом Гаусса

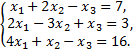
Составим по данной системе расширенную матрицу

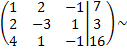
умножим первую строку на 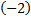и сложим со второй строкой; умножим первую строку на и сложим с третьей строкой, получим

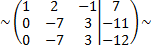
умножим вторую строку на 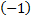и сложим с третьей строкой

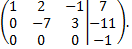
В данном случае последняя строка противоречива, так как 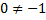, следовательно, система несовместна.