Ранг матрицы. Ранг матрицы – это наивысший из порядков миноров матрицы отличных от нуля.

Ранг матрицы – это наивысший из порядков миноров матрицы отличных от нуля.

Обозначение ранга матрицы 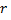или

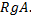
Матрицы, полученные в результате элементарного преобразования, называют эквивалентными матрицами.

Очень важным свойством элементарных преобразований матриц является то, что они не изменяют ранг матрицы.

Ранг матрицы равен числу ненулевых строк в матрице, приведенной с помощью элементарных преобразований к треугольному (ступенчатому) виду.

Рассмотрим пример. Определить ранг матрицы

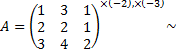
Тогда

Или

следовательно, ранг матрицы

Контрольные вопросы

1. Какая матрица называется обратной?

2. Пояснить алгоритм вычисления обратной матрицы.

3. Дать определение системы линейных алгебраических уравнений. Что называется ее решением?

4. Для каких систем применимо правило Крамера?

5. Записать формулы Крамера.

6. Пояснить алгоритм решения систем методом обратной матрицы.

7. Дать определение ранга матрицы.