Обратная матрица

Рассмотрим квадратную матрицу

Матрица A называется невырожденной, если ее определитель отличен от нуля. Если определитель матрицы равен нулю, матрица называется вырожденной.

Для невырожденной матрицы A существует обратная матрица 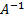, которая в произведении с матрицей A дает единичную матицу:

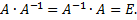
Обратная матрица вычисляется по формуле:

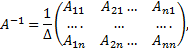
где 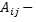алгебраические дополнения к элементам матрицы, -определитель матрицы.

Элементы матрицы заменяют алгебраическими дополнениями, полученную матрицу транспонируют и каждый элемент делят на определитель.

Рассмотрим пример. Найти обратную матрицу 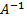к матрице

Рассмотрим алгоритм решения. Первый шаг, найдем главный определитель матрицы

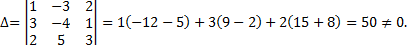
Следовательно, 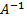существует.

Второй шаг, транспонируем исходную матрицу

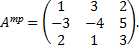
Третий шаг, найдем алгебраические дополнения для каждого элемента транспонированной матрицы

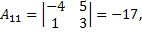
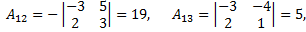
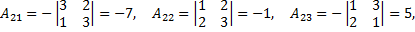
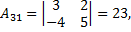
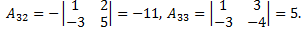
Последний шаг, записывают матрицу обратную исходной матрице

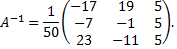
Проверим полученный результат:

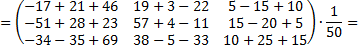
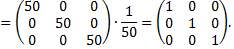
По полученному результату можно сделать вывод, что обратная матрица 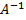матрице 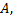найдена правильно.